Universal Set
Table of Content |
|
|
Meaning of Universal Set
As a set is a collection of different objects having some common property, the universal set is the collection of all the elements related to particular topic. It could be anything like natural numbers, a pack of cards, people in the world, etc. Here universe doesn’t mean anything in the world but all the things relate to our problem.
Definition of Universal Set in math
Universal set is the superset of all the elements under consideration. If we are talking about no. of people in India, China and Japan then the universal set will be the set of all the people of these three countries.
N = {1, 2, 3, 4, 5,…}
A = {1, 3, 5, 7,…}
B = {2, 4, 6, 8,…}
Here in Set A and B we are talking about the odd numbers and even numbers so N i.e. the set of natural numbers will be the universal set of A and B. As it includes all the elements of A and B.
Universal Set symbol
-
Universal set is generally represented by capital letter “U”.
-
It’s all the subsets by other capital letters like X, Y, Z, etc.
-
We have to list all the elements of universal set then enclose them in the curly braces “{ }”.
-
Ellipses (…} i.e. three dots are used to represent the sets if it is infinite set or a finite set with large number of elements.
Universal set
U= {1, 2, 3, 4,…}
Is Universal Set Finite or Infinite?
Universal set could be both Finite and Infinite.
Finite Set
Finite Set is a set which has limited or countable number of elements. As if we are talking about a set of vowels then the universal set for it will be a set of all alphabets which is a finite set having 26 elements in it.
Example
U = {a, b, c,…, x, y, z}, it is the universal set for our consideration.
V = {a, e, i, o, u}
Here we have used the ellipses as it is set with large number of elements.
Infinite Set
Infinite Set is a set which has unlimited number of elements. We use the ellipses in the starting or the end of the set or both sides to show the infinity of the set. If we are talking about numbers then its universal set could be set of natural numbers, set of all real numbers which are infinite set.
Here we have used ellipses at the both sides as this set is unlimited from both ends.
Universal Set and its Subsets
A set X is a subset of Y if all the elements of X are the elements of Y also. It is represented by “⊆” means “is a subset of”.
X⊆Y if x∈X⇒x∈Y
And a set X is said to be proper subset of Y if all the elements of X are the elements of Y but all the elements of Y are not the elements of X.
It is represented by “⊂” means “ is a proper subset of”.
As universal set is a set having all the elements regarding the topic of consideration, all the other sets in it are the subsets of Universal set.
It is important to note that as all the sets are the subset of itself universal set is also the subset of itself.
U⊆U that is. universal set is a subset of itself.
The subsets of an infinite universal set could be finite or infinite both.
Example
U = {1, 2, 3, 4,…}
A = {1, 2, 3}
B = {4, 5, 6}
Here universal set is the set of all natural numbers.
A is the subset of U as all the elements of A are the elements of U also.
A⊂U
B is also the subset of U as all the elements of B are also elements of U.
B⊂U
But there is no common element in A and B so these are two disjoint set of U.
A∩B=∅
Here A and B are the finite sets.
But there could be some other subsets of U also, like,
X = {1, 3, 5, 7,…} i.e. a set of all odd numbers.
Y = {2, 4, 6, 8,…} i.e. a set of all even numbers.
X⊂U and Y⊂U and both are the infinite sets.
Equivalent Sets
Two sets are called Equivalent Sets if there number of elements are same .The elements need not to be same, just the number of elements should be same.
Properties of Equivalent Sets
- Sets are said to be equivalent if there cadinality (size or the number of elements) is same.
If A = {a, e, i, o, u} and B = {5, 6, 7, 8, 9}
Then set A is equivalent to set B as there number of elements are same.
-
As all the empty sets has zero cardinality, so all the empty sets are equivalent sets.
-
Two sets are equivalent if there is bijection within two sets. The bijection is the one to one correspondence between two sets.It means that for every elemnet in Set A there must be an element in Set B, till the elements get over.
-
To represent equivalent sets we use equivalent sign "~" or “ ≡ "
-
Equal Sets are equivalent also. Two sets are said to be equal if their elements and the number of elements are exactly same. And said equivalent when only their number of elements is same. So, the two equal sets will always be equivalent.
-
Equivalent Sets may not be equal sets. As equivalent sets have same cardinality but the elements may be different. In the above picture
A~B but A ≠B
Set A is equivalent to Set B as there number of elements are same but A is not equal to B as there elements are different.
Universal Set and Venn Diagram
Representation of Universal Set
Venn diagram is the graphical representation of sets. It is the easy way to understand the sets.
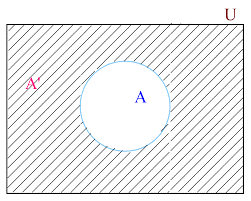
In Venn diagram the universal set is represented by rectangle and denoted by U and its subsets by circles and denoted by capital letters as “A” in the given picture.
Subsets of Universal Set
The elements of the sets should be written in circle of that particular set. According to the elements we can see the relation between the different subsets of a universal set.
Here, A = {1, 5, 6, 7, 8, 9, 10} that is. all the elements in Set A
B = {2,3,4,6,7,9,11,12,13} that is. all the elements in se B
A∪B that is. A union B means all the elements that are in Set A and Set B or Both.
A∪B = {1, 2, 3, 4, 5, 6, ,7, 8, 9, 10, 11, 12, 13}
A∩B i.e. A intersection B means all the elements that are common in both sets.
A∩B = {6, 7, 9, 12}
A and B are the joint sets as there are some elements common between them.
Universal Set and complement of set
If U is the universal set and A is the subset of U then a set of all the elements that are not the member of A is called complement of Set A.
The complement of set A is denoted by (A′).
As in the above picture the rectangle shows the universal set and A is the subset of U. Here the entire shaded portion is the complement of A means all the elements that are not in A.
Symbolically,
We can read it as A′ is a set of elements which belongs to U but not belongs to A.
Or you can say
A′ = U - A
Complement of a Universal Set
As universal set is the set of all the elements regarding our consideration then there is no element left without it. So, the complement of a universal set is always empty set.
Empty set is a set with no element or zero cardinality. If we are talking about a set of all prime numbers then the universal set for our consideration will be,
U = {1, 2, 3, 5, 7, 11, 13,…}
As there is no prime number left, the complement of this set will be { } i.e. empty set. As complement of U is the set of all the elements which are not the element of U.
U′ = {x: x U} = ∅
Vice versa we can say that the complement of an empty set is the universal set.
Example
What is the B′ (complement of Set B) in the given picture?
Solution
In the given picture,
U = {0,1, 2, 3, 4, 5, 6, 7, 8, 9} that is. the universal set in the given example, contains all the elements.
B = {2, 4, 6, 7, 8} that is. all the elements in Set B.
B′ = U – B = {0, 1, 3, 5, 9} that is. all the elements that are not the element of B.
B is the subset of U and B′ is also the subset of U as all the elements of B and B′ both are the elements of U also.
B∩B′ = ∅, there is no common element within them so these are disjoint sets.
U′= ∅ that is. complement of U is Empty set as there is no element left without consideration.
Complement of the Complement of a Set
If A is the subset of U then A′ is also the subset of U, as all the elements of A and A′ both are the elements of universal set.
A set and the complement of a set are two disjoint sets. The disjoint sets are those sets which have no common element within them. So as A and A′ has no common element within them, these are the two disjoint sets.
Example
Let U = {a, e, i, o, u} and A = {a, e}
A′= {i, o, u} i.e. all the elements which are not the elements of A.
Hence, (A′)′ = A′={x: x∈U and x∉A′}
= {a, e} = A
This shows that the complement of the complement of a set is the set itself.
(A′ )′ = A
More Readings