Venn Diagrams

Definition of Venn Diagrams

Venn Diagrams is basically the graphical representation of sets. Set is the collection of different things and Venn diagram shows the relation between different sets. It makes the problems related to sets easy as it is used to solve the problems related to sets. It is also called set diagram or logic diagrams. Generally, we don’t draw a proportional Venn Diagrams. The Venn diagram in which the shape is proportional to the number of elements is called Scaled Venn Diagrams.
 

Sets

As the Venn Diagram is the representation of sets, so we need to brief the meaning of sets first. A set is a collection of different objects having some common property and all the objects are the elements of set. For example, the numbers 1, 2 and 3 are different numbers separately but collectively they form a set of three numbers {1, 2, and 3}. If we can decide that a particular object belongs to the given collection, then it is a set of those objects. We have to list each element separated by a comma, and then put curly brackets around it. These curly brackets { } are also called "Braces”. The repetition of elements and the order of elements have no relevance in the set.

Universal Set

Universal Set is the important part in Venn Diagram. The basic sets of numbers are called the universal sets. As the set of all the natural numbers, set of all prime numbers etc. are the universal sets. Or you can say that anything which is there in the consideration comes in the universal Set.  It is shown by U.
 

Representation of Sets with Venn Diagrams

• Venn Diagrams are generally represented by rectangle which is called the Universal Set of the topic in consideration and denoted by capital letter “U” or “E”.

• It’s all the subsets are represented by the closed figure like circles and represented by other capital letters like X, Y, Z, etc.

• The elements of the sets are to be written in the respective circles.

Here in the above picture,

The rectangle shows the universal set which contains all the elements under consideration.

U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

The circles represent the subsets of the universal set. And denoted with the capital letters.

A = {1, 2, 3, 7, 9, 11}

B = {3, 4, 6, 7, 11}

The circles could be separate or overlapping depends upon the relationship between them.

The overlapping shows the common elements within the sets.

Both A and B has 3 elements in common that is. 3,7,11.

There are some elements left which are not the elements of A nor B. But are the elements of U.
 

Relation between different Sets

Union of two sets

The union of two sets A and B is the set of all the elements present in A or B or both. We will take the common elements at once only. It is denoted with the symbol “∪” read as “union”.

• Union of two Joint Sets: Joint sets are those which have some common elements within them. It is shown by two overlapping circles.

A∩B ≠ ∅ that is. A intersection B is not an empty set.

Here,

∪B = {1, 2, 3, 4, 5, 6} read as “A union B”.

It contains all the elements of A and B both.

A = {1, 2, 3, 4, 5} that is. n(A) =5

B = {2, 4, 6} that is. n(B) =3

But here n(A) +n(B) ≠ n(A∪B) because the 2 elements are common and they will be counted twice. So we can say that n(A) +n(B)-n(A∩B) = n(A∪B), where A∩B is the common element within the two sets. 

• Union of two Disjoint Sets: Disjoint Sets are those which have no common element within them, as the name represents; these are two separate sets and does not overlap each other.

A∩B = ∅ that is. A intersection B is an empty set.

Here, A and B are two disjoint sets.

A = {a, b, c}

B = {d, e, f, g}

A∪B = {a, b, c, d, e, f, g} that is. all the elements present in both A and B.

In the case of disjoint sets n(A)+n(B) = n(A∪B) as there is no common element within them.

Intersection of two Sets

The Intersection of two sets A and B means a set of all the elements which are common to both A and B. It is represented by symbol “∩” reads as “Intersection”.

Here Set P contains people who has cat as a pet.

P = {6,10}

Set B contains people who have dogs as pet.

B = {8,10}

And the yellow area shows the common people who has both cat and dog as pet.

P∩B = {10} reads as P intersection B.

Intersection of two disjoint sets will always be empty set as there is no common element within the two disjoint sets.

A∩B = ∅ if A and B are two Disjoint Sets.
 

Complement of a Set

The complement of a set A is the set of all the elements which are the elements of Universal set but not the elements of A. It is represented by A′.

Here,

U = {1, 2, 3, 4, 5, 6, 7, 8, 9}

A = {2, 3, 4, 5, 6}

A′ = {1, 7, 8, 9} that is. all the elements which are not present in A.

Or you can say A′=U-A

A′ is represented by the shaded portion in the above picture.

Both A and A′ are the subsets of Universal set. And both are the two disjoint sets as there is no common element within them.

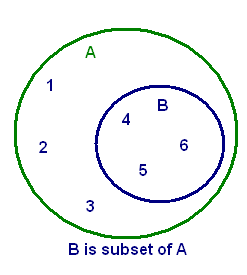
Subset of a Set

A set X is a subset of Y if all the elements of X are the elements of Y also. It is represented by “⊆” means “is a subset of”.

X⊆Y if ∈ X⇒∈Y

Here in the above picture blue circle represents the subset of A and green circle represents the superset of B.

A = {1, 2, 3, 4, 5, 6}

B = {4, 5, 6}

B⊂A that is. all the elements of B are the elements of A.

Difference of Sets

The difference of two sets A and B represents as A-B that is. all the element which are present in A but not in B.

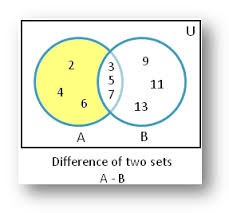Here in the above picture yellow portion shows the difference that is. A-B.

A = {2, 3, 4, 5, 6, 7}

B = {3, 5, 7, 9, 11, 13}

A-B = {2, 4, 6}

A-B is not necessarily equal to B-A.
 

Venn Diagrams with 3 circles

This is the extension of two circle Venn Diagrams. This is the overlapping of three circles. Let’s try to understand the relationship of three sets with three circles Venn Diagrams.

n(T) = 2 + 3 + 9 + 10 = 24

Number of people enrolled for tennis.

n(J) = 4 + 4 + 9 + 10 = 27

Number of people enrolled for Jogging.

n(S∩T) = 9 + 3 = 12

Number of people enrolled for both swimming and tennis.   

n(S∪T) = n(S) + n(T) – n(S∩T)

= 35 + 24 – 12=47

Number of people enrolled for swimming or tennis or both.

n(T∩J) = 9 + 10 = 19

Number of people enrolled for both tennis and jogging.

n(T∪J) = n(T) + n(J) – n(T∩J)

= 24 + 27 – 19 = 32

Number of people enrolled for tennis or jogging or both.

n(S∩J) = 9 + 4 = 13

Number of people enrolled for both swimming and jogging.

n(S∪J) = n(S) + n(J) – n(S∩J)

= 35 + 27 – 13 = 49

Number of people enrolled for swimming or jogging or both.

n (S ∩ T ∩ J) = 9

Number of people enrolled for all the three sports.

n(S∪T∪J) = n (S) + n (T) + n (J) - n (S ∩ T) – n (T ∩ J) - n (S ∩ J) + n (S ∩ T ∩ J)

= 35 + 24 + 27 – 12 – 19 – 13 + 9

= 51

Number of people enrolled for swimming or tennis or jogging or any of the sport.

(S∪T∪J)′ = 9

Number of people who didn’t enroll for any of the sport.

More Readings

Venn Diagrams