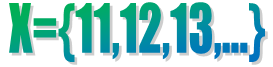Sets and Their Representations

 

Table of Content

Introduction to Sets and Their Representations Sets in Mathematics Basic Functions and Properties of Representing Sets Sets and Their Representations Roster or Tabular Form Descriptive or Statement Form Set-builder or Rule Form Standard Sets Let’s Try Some Question Related to Representation of Sets Graphical Representation of Sets

Intoduction of Sets and their Representations

In our day to day life, we always talk about collection of different things like a group of students, group of shapes, members of football team etc.

Anything which has some common property could be clubbed in a group. That group is called a set.

Basically, Set is a collection of things which have some common features.

 

Sets in Mathematics

In mathematics, also we could have different types of collections like

• Collection of solution of any problem

• Collection of number of alphabets in English

• Collection of factors of any number

• Collection of different shapes, etc.

 

Basic Functions and Properties of Representing Sets

As you know that a SET is an exact collection or you can say a well-defined collection of discrete or distant objects, there are some rules which we need to follow to write down the sets, so that it could be understand easily.

The numbers 2, 4, 6 and 8 are different numbers separately but collectively they form a set of four even numbers less than 10 i.e., {2, 4, 6, and 8}. If we can decide that a particular object belongs to the given collection, then it is a set of those objects

As here 2, 4, 6, 8 are the objects having common property that these are even number, so they form a group.

Here we can say that 8 belong to this group but 9 does not belong to this group.

Properties

• Sets are written with capital letters.

Example:

Set A, Set Y, Set T etc.

• The Elements of a set are written with small letters.

Example:

a, y, t, etc.

The elements and members are the same things.

• We have to list each element separated by a comma, and then put curly brackets around it

Example:

These { } are also called "braces".

• The number of elements are denoted as

n(A)=4 , as in the above picture the number of elements are 4.

• If there are three dots in a set it means it is an infinite set.

The three dots here ... are called an ellipsis and it means "continue on".

• These three dots can be used in between also for the long listings.

Example:

{1, 2, 3,…, 99,100} It is a definite set as it has 100 natural numbers in it.

• If b is an object or element of set B, we read it as “b belongs to B”

For which, we use the Greek symbol ∈ (epsilon), which means ‘belongs to’.

Thus, we will write b∈B. If ‘c’ is not an element of set B, we write c∉B and read “c does not belong to B”.

Example:

In the above picture,

1. A set is denoted by “N”, which is a capital letter.

2. The elements of the set N are 1,2,3,4,5,6,7,8,9.

3. The elements are separated with comas and are enclosed in the braces.

So, we write it as N= {1,2,3,4,5,6,7,8,9}

4. It shows that 4 is an element of Set N, but 12 is not an element of Set N.

So, we write it as 4∈ N but 12∉N

 

Sets and Their Representations

Sets can be represented by three methods:

 

Roster or Tabular Form

In this form, we have to list all the elements of a particular set, then separate with commas and write them within the curly brackets { }.This form is also called extensional definition.

Example:

T = {January, June, July}, a set of the months in a year starting with letter J.

S = {Saffron, White, Green}, a set of the colors of Indian flag.

Some important points about roster method to be noted are-

1. The element should not be repeated in this form. If you have a set in which there are two same elements, then you will write it only one time.

Example:

F= {25, 25, 30, 30}

Then you will write it as, F= {25, 30}. The meaning of both the sets will remain same.

2. The order of the members of a set also does not have any relevance. So, you can write the elements of a set in any Sequence.

As in the above example, you can write it as, F= {30, 25}, Here the meaning will remain same.

So that,

F= {25, 30} = {30, 25} = {25, 25, 30, 30}

 

Descriptive or Statement Form

In this form, we just have to give the description of the elements of the sets in a statement form.

Example:

• L is a set of number of students in class VIII.

• M is a set of different 3D shapes.

• N is a set of all natural numbers less than 20 which are divisible by 4.

• O is a set of all the alphabets in English.

 

Set Builder or Rule Form

All the elements of a set which are having some common property, which is not contained by any other element outside that set is shown by set builder form. This is just the extension of descriptive form. The descriptive form and set builder form altogether comes in Intentional definition.

The element of that set is denoted by a symbol ‘y’ or any other variable(w, v,..) followed by ‘:‘(colon) or ‘|‘ , which means “such that” and then we have to  write the property of the elements of the set using symbols and write the whole description in brackets. 

For example: 

Let E is the set of all natural even numbers greater than 15;

The set A in set-builder form is a follows: 

E = {x: x is a natural even number which is greater than 15}

or

E = {x | x is a natural even number which is greater than 15}

or

E ={ x | x is a natural even number, x ≥15}

or

E = { x | x ∈N even number, x ≥15}.

This shows that E is a set of elements (x) such that x is a natural number which is greater than 15 also'.

 

Standard Sets

Some standard sets of numbers are there in mathematics, which can be represented in all the three form of sets, that is, Roster form, Statement form and set builder form.

No.	Standard set
	N= Natural numbers	Roster from Description form Set builder form	N={1,2,3,…} N is the set of all natural numbers. N={n:n is a natural number}
	Q=Rational numbers	Roster from Description form Set builder form	Q={1/2,2/3,3/4,…} Q is the set of all rational numbers. Q={q:q is a rational number}
	R=Real numbers	Roster from Description form Set builder form	R={-∞,…, ∞} R is the set of all real numbers. R={r:r is a real number}
	P=Prime numbers	Roster from Description form Set builder form	P={1,2,3,5,7,11,…} P is the set of all prime numbers. P={p:p is the prime number}
	Z or I=Integers	Roster from Description form   Set builder form	Z={…,-2,-1,0,1,2,…} Z is the set of all negative and positive of natural numbers and zero also.   Z={z:z is a real number}
	E=Even integers	Roster from Description form   Set builder form	E={2,4,6,8,…} E is the set of natural numbers which are divisible by 2.   E={e:e∈ N and e=2n}
	O=Odd integers	Roster from Description form   Set builder form	O={1,3,5,7,…} O is the set of natural numbers which are not divisible by 2.   O={o:o∈ N and o=2n+1}

Therefore, almost every standard set of numbers can be expressed in all the three methods as discussed above.
 

Let’s Try Some Question Related to Representation of Sets

Example 1	Write the given numbers 1, 3,5,7,9 in all the three form of sets.
Solution 1	Let A is the name of the set. The numbers 1, 3,5,7,9 are the odd natural numbers less than 10. So we can write it as, Description form: A is the set of odd natural numbers less than 10. Roster form: A={1,3,5,7,9} Set builder form: A={y:y is an odd natural number and y<10}

 

Example 2	How can we write the colors of rainbow in all the three form of sets?
Solution 2	Let R is the name of the set. So we can write it as, Description form: R is the set of all colors of the rainbow. Roster form:R={violet, indigo, blue, green, yellow, orange, red} Set builder form:R={y:y is a color and y is the color of rainbow}

Here, we have written the sets in all the three forms of representation of sets, but sometimes it is practically not possible to list all the elements of the set. At that time we should use the describing method.

Example: How can we represent the set of pet animals?

As there are n numbers of pet animals, so it is not possible to list all the pet animals name as the element of set.

Here, it is better to use description method.

A is the set of all pet animals.

If we want to write it in Roster form, we can write it as,

A= {Dog, Parrot, Cat, Tortoise, Fish, Rabbit,…}

Let’s see how can we write the following sets in roster form?
	Given sets	Roster form
	L = {x : x is an integer and –5 < x < 5}	L={,-4,-3,-2,-1,0,1,2,3,4}
	M = {x : x is the first four month in a year}	M={January,February,March,April}
	N = {x : x is a natural number which is divisible by 11 and less than 100}	N={11,22,33,44,55,66,77,88,99}
	O = The set of all letters in the word ARITHMETIC	O={A,R,I,T,H,M,E,C}
	P=The set of vowels in English alphabet	P={a,e,i,o,u}

 

Graphical Representation of Sets

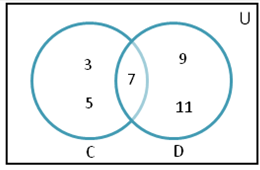
The sets can be represented in graphical form also through Venn diagram which shows the relationship between different sets. It is the easiest way to read and understand sets.

In the above picture:-

• The universal set is represented by rectangle.

• Their subsets are represented by circles.

• The elements of sets must be written in circles.

Here, we will write the sets like,

C= {3, 5, 7}

D= {7, 9, 11}

And the element which is present in both the sets is 7.

So it is the easiest way to represent the relation between different sets.

To know more about Venn diagram, click here: Venn diagrams

More Readings

Sets and Their Representations