Subsets

 

Table of Content

Definition of Sets Definition of Subsets Symbol of Subset Proper Subset Relation between Subset, Proper Subset and Superset Is Every Set a Subset of itself? Empty Set is a Subset of every set Other Important point about Subset Number of Subsets Formula for calculating the number of Subsets Subsets of Set of real numbers

Definition of Sets

To understand the concept of subsets, first we need to recall, what is sets? A set is a collection of different things having some common 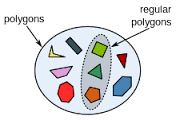property, not necessarily. The objects of a set are called the elements of a set. These elements have their own identity separately but collectively they make a set.

We have a set of 9 polygons here, but we can make a set of regular polygons only also. Or we can make a set of triangles also. So, we must be able to differentiate all elements from each other.
 

Definition of Subsets

A set A is said to be a subset of set B, if all the elements of set A are the element of set B also. Or we can say that a Set A is the subset of set B if x belongs to A means X belongs to B also.

Here all the elements of set A are there in set B. So, A is a subset of B. We can also say that B contains A, so B is the superset of A.

Example

A = {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}

B = {Monday, Tuesday, Wednesday}

Here, all the elements of B are present in A, so B is the subset of A.
 

Symbol of Subset

To represent the subset we use a symbol “⊆” it means “is a subset of”.

As in the above example B⊆A i.e. B is the subset of A.

For the superset we use the symbol “ ⊇” it means “ is a superset of”.

A ⊇B i.e. A is the superset of B or A contains B.

If X is not a subset of Y then we write it with Symbol “⊈” it means “ is not a subset of”.

We write it as X⊈Y i.e. X is not a subset of Y.

Symbolically we can write the definiton of subset as follows-

A⊆B if x A  x B

We can read it as “A is the subset of B if x belongs to A implies that x also belengs to B.
 

Proper Subset

If X is the subset of Y but Y is not the subset of X, then X is the proper subset of Y .Or If all the elements of X are present in Y but all the elements of Y are not there in X. Then X is the proper subset of Y.And Y is the proper superset of X.

We denote it with the symbol “⊂” it means “is a proper subset of”.

And “⊃” it means “is a proper superset of”.

Example

Here,

A = {1, 2, 3, 4, 5, 6}

B = {4, 5, 6}

It shows that all the elements of B are the elements of A also but all the elements of A are not there in B. So B⊂A i.e. B is the proper subset of A.
 

Relation between Subset , Proper Subset and Superset

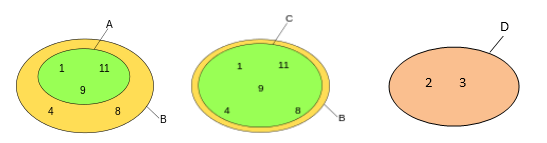
A = {1,9,11}

B = {1,4,8,9,11}

C = {1,4,8,9,11}

D = {2,3}

This shows that:

• A⊂B i.e. A is the proper subset of B as All the elements of A are the elements of B but all the elements of B are not the elements of A.

• B⊃A i.e. B is the proper superset of A as B contains A but A does not contain B.

• B⊆C i.e. B is the subset of C but not the proper subset of C as B = C.

• C⊇B i.e. C is the superset of B as C contains B.

• D⊈B i.e. D is not the subset of B as all the elements of B and D are different.
   

Is Every Set a Subset of itself?

If X is the subset of Y, then all the elements of X are there in Y but it is not necessary that all the elements Y are also there in X . But if It happens than Y is also the subset of X. It means that X and Y are same sets i.e. equal sets.Two sets are said to be equal sets if there elements and the number of elements are exactly same.

Symbolically,

X⊆Y and Y⊆X ⇔ X=Y

“⇔” it represents the two way implication, it means “if and only if”.

We read it as X is the subset of Y and Y is the subset of X if and only if X is equal to Y.

As in the above picture it shows that X and Y have same elements , so they are equal sets . It simply means that both are same sets. As X =Y, X⊆X and Y⊆Y.

So every set is a subset of itself.
 

Empty Set is a Subset of every set

Empty Set is a set with no element in it .It is a set with zero cardinality i.e. the number of element is zero (0). The symbol of empty set is { } or ∅ (phi).It is also called Null or Void Set.

If all the elements of a set X are present in set Y, then X will be a subset of Y, so if all the elements of the empty set are present in any set then it will be a subset of that particular set. 

Example

X= {1, 3, 5, 7}

Here, Set with 0 elements in this set is 1 i.e.-∅ (empty set)

As empty set is a set which have no element in it, so it can be easily present in any set.

This shows that empty set is the subset of every set.

∅⊆X

Empty set is a subset of every set and every set is a subset of itself. So, Empty set is also a subset of itself.

∅⊆∅

But the empty set is not the proper subset of itself. The empty set is a proper subset of all sets except ∅.

∅ ⊂X≠ ∅

We read it as; empty set is a proper subset of X which is not equal to empty set.
 

Other Important point about Subset

Here in the above picture, it shows that A is the subset of B as all the elements of A are there in B and B is the subset of C as all the elements of B are there in C.

It represents that if,

A⊂B and B⊂A ⇒ A⊂C

We will read it as If A is the subset of B and B is the subset of C it implies that A is the subset of C also.

Example

X = {0,1,2,3,5,6}

Y = {1,2,3,4,5}

Z = {2,3,4}

Here,

Z⊂Y and Y⊂X ⇒ Z⊂X

It shows that Z is the subset of Y and Y is the subset of X so Z is also the subset of X.
 

Number of Subsets

V = {1, 2, 3, 4, 5}

Here set V has 5 elements. Let’s see the possible subsets of this set:

∅	{1}	{1,2}, {1,3}	{1,2,3}, {1,2,4}	{1,2,3,4,5}
	{2}	{1,4}, {1,5}	{1,2,5}, {1,3,4}
	{3}	{2,3}, {2, 4}	{1,3,5}, {1,4,5}
	{4}	{2,5}, {3, 4}	{2,3,4}, {2,3,5}
	{5}	{3,5}, {4,5}	{2,4,5}, {3,4,5}

 

	Number of subsets
Subsets with 0 element	1
Subsets with 1 element	5
Subsets with 2 elements	10
Subsets with 3 elements	10
Subsets with 4 elements	5
Subsets with 5 elements	1
Total number of subsets	32

Real numbers is a set of all possible numbers in the universe.So all the other sets of numbers are the subsets of real numbers.

More Readings

Subsets