Complement of a Set
Table of Content |
|
|
Meaning of Complement
Complement is something which makes anything perfect or one of the two parts needed to complete the counterpart.
Example
If we are talking about the total number of students in a school, it could be divided in two parts i.e. number of boys and number of girls. Here number of boys is the complement of number of girls as boys and girls together makes the total number of students in that particular school.
In mathematical terms we can say that total number of students is the universal set, number of boys is one subset of universal set and number of girls is the complement of number of boys.
So to understand the concept of complement of sets first we need to understand the concept of sets, universal sets and the subsets.
What is the meaning of Sets in mathematics?
A set is a collection of well defined objects which have some common property (not necessarily). The objects are the elements of sets.
The sets are represented as:
-
The sets are represented by capital letters.
-
The elements are generally represented by small letters.
-
List all the elements.
-
Separated them with comma.
Example
Note: The order and the repetition of elements have no relevance here. The meaning will remain same.
Subset
Whenever we talk about sets there will always be the subset of the sets. As all the elements of sets have their own separate identity so they make the subsets of the sets.
A set X is a subset of Y if all the elements of X are the elements of Y also. It is represented by “⊆” means “is a subset of”.
X⊆Y if x∈X ⇒ x∈Y
There could be so many possible subsets of a set.
Example
A = {2, 4, 6, 8}
It’s possible subsets are:
Subsets with 1 elements = {2}, {4}, {6}, {8}
Subsets with 2 elements = {2, 4}, {4, 6}, {6, 8}, {8, 2}, {2, 6}, {4, 8}
Subsets with 3 elements = {2, 4, 6}, {4, 6, 8}, {6, 8, 2}, {2, 4, 8}
Subsets with 4 elements = {2, 4, 6, 8}
Universal Set
The basic sets of numbers are called the universal sets. Like the set of all the natural numbers, set of all prime numbers etc. are the universal sets. Or you can say that anything which is there in the consideration comes in the universal set. It is the superset of all the sets under 
consideration. It is denoted by “U”.
Universal set in Venn diagram is generally represented by:
-
Rectangle and denoted by U
-
Its subsets by circles and denoted by capital letters as “A” and “B” in the given picture.
-
All the elements of the sets are to be written in the respective circles.
What is the definition of Complement in Math?
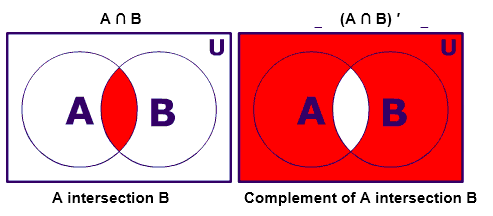
The Complement of a Set A is the set of all the elements which are the elements of Universal set but not the elements of A. It is represented by symbol A′ or Ac.
Symbolically,
A′ = {x: x U, x A}
A′ = U-A
A′ is represented by the shaded portion in the above picture. This shows all the elements which are not the elements of A.
Both A and A′ are the subsets of Universal set. And both are the two disjoint sets as there is no common element within them.
U = {x: x N} that is, the set of all natural numbers
A = {x: x O} that is, the set of all odd natural numbers.
A′ = {x: x E} that is, the set of all even numbers.
Types of Complement of Sets
There are two types of complement of sets:
-
Relative Complement(difference of sets)
-
Absolute Complement
Relative Complement (Difference of Sets)
The Relative Complement of set A with respect to set B is the set of all the elements present in B but not in A. It is also called the difference of two sets A and B represents as “A-B”. Here we are talking about the relation of complements of set A and B only not related to universal set.
Here in the right picture green portion shows the difference that is, A-B.
A-B = {x: x∈ A and x∉ B} = A∩B′
Vice versa, yellow portion shows, B-A
B-A = {x: x∈ B and x ∉ A} =B∩A′
Example
A = {2, 3, 4, 5, 6, 7}
B = {3, 5, 7, 9, 11, 13}
A-B = {2, 4, 6}
B-A = {9, 11, 13}
A-B is not necessarily equal to B-A.
Relationship between set differences
A′-B′ = B-A
Properties of Relative Complement: There are two types of properties of Relative Complement
-
Complement Laws
-
Difference Laws
Complement Laws :
A-A = ∅
This shows that A –A will always be an empty set.
A-∅ = A
A-∅ will always be the set itself.
∅-A = ∅
∅ -A will always be the empty set
Difference Laws:
A-(∪C) = (A-B) ∩ (A-C).
A-(B∩C) = (A-B) ∪ (A-C)
Absolute Complement
Absolute complement is simply the complement of A that is, the set of all the elements present in U but not in A. It is the relative complement of A in U. So we can say that complement of A is,
A′ = U-A
A′ = {x: x U, x A}
Here all the other sets like B do not have any relevance as we are talking about A and U only.
Properties of Absolute Complement: There are four types of properties of Absolute Complement
-
Complement Laws
-
Law of empty and Universal Set
-
Double Complement Law
-
De Morgan’s Law
Complement Laws:
A∪A′=U
The union of the set and its complement will always be the universal set as both are the subset of universal set and together they contain all the elements of universal set.
A∩A′ = ∅
The intersection of the set and its complement will always be the empty set as these are two disjoint sets and they have no common element within them.
Law of empty and Universal Set:
U′={x: x U} =∅
As universal set is the set of all the elements regarding our consideration then there is no element left without it. So the complement of a universal set is always empty set.
∅′ = U
The complement of the empty set is universal set.
If A⊂B then B′⊂A′
Double Complement Law:
If A is the subset of U then A′ is also the subset of U, as all the elements of A and A′ both are the elements of universal set.
Let U = {a, e, i, o, u} and A = {a, e}
A′= {i, o, u} that is, all the elements which are not the elements of A.
Hence, (A′)′ ={x: x∈U and x∉A}′
= {a, e} =A
This shows that the complement of the complement of a set is the set itself.
(A′ )′ = A
De Morgan’s Law:
De Morgan's laws are a pair of transformation rules. They are named after Augustus De Morgan.
De Morgan’s Law of Union
It can be expressed in English as,
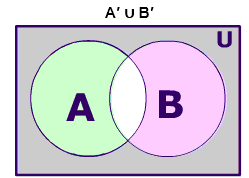
The complement of the union of two sets is the same as the intersection of their complements.
It can be expressed in Boolean algebra as,
(A ∪ B)′ = A′ ∩ B′
Let’s try to prove the expression.
Left hand side
Right hand side
Intersection of complement of A and the complement of B
As the last image of both left hand side and the right hand side is same.
Hence this proves that (A ∪ B)′ = A′ ∩ B′
De Morgan’s law of intersection
It can be expressed in English as,
The complement of the intersection of two sets is the same as the union of their complements.
It can be expressed in Boolean algebra as,
(A ∩ B)′ = A′ ∪ B′
Let’s try to prove the expression
Left hand side
Right hand side
Union of complement of A and the complement of B
As the last image of both left hand side and the right hand side is same.
Hence this proves that
(A ∩ B )′ = A′ ∪ B′
Complement of a Set vs. Complement of a Universal Set
Here in the above Venn diagram the universal set is the set of natural numbers less than 10. So,
U = {1, 2, 3, 5, 6, 7, 8, 9} i.e. the set of all the numbers in our consideration.
A = {1, 3, 5, 7, 9}, A⊂U, A is the set of odd natural numbers less then 10. So A is the subset of U.
A′ = {2, 4, 6, 8}, A′⊂U, A′ is the set of even natural numbers less than10. So A′ is also the subset of U.
Here the complement of Set A is the set of all the other numbers which are the elements of U but not of A.
Symbolically,
A′ = {x: x∈U, x∉A} that is, all the elements of A′ are the elements of U but not the elements of A, as shown in the above example.
And the complement of the universal set will be null set as universal set contains all the elements under consideration so there is no element left to consider for the complement of universal set and vice versa. So
U′=∅
∅′ = U
Let’s solve one problem related to Complement of Sets
Example
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, X = {1, 2, 3, 4}, Y = {2, 4, 6, 8} and
Z = {3, 4, 5, 6}.
Find the complements of X, Y Z, unions and intersections.
Solution
U = {1, 2, 3, 4, 5, 6, 7, 8, 9} U′ = ∅
X = {1, 2, 3, 4} X′ = {5, 6, 7, 8, 9}
Y = {2, 4, 6, 8} Y′ = {1, 3, 5, 7, 9}
Z = {3, 4, 5, 6} Z′ = {1, 2, 7, 8, 9}
X∪Y = {1, 2, 3, 4, 6, 8} (X∪Y) ′= {5, 7, 9}
Y∪Z = {2,3,5,6,8} (Y∪Z) ′.= {1,4,7,9}
Z∪X = {1,2,3,4,5,6,} (Z∪X)′ = {7,8,9}
X∩Y= {2, 4,} (X∩Y) ′= {1, 3, 5, 6, 7, 8, 9}
Y∩Z = {4,6} (Y∩Z) ′.= {1,2,3,5,7,8,9}
Z∩X = {3,4} (Z∩X)′ = {1,2,5,6,7,8,9}
More Readings
Complement of a Se