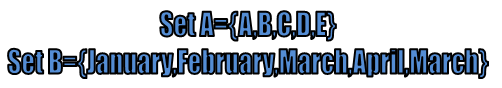Introduction of Sets

 

Table of Content

From where the Concept of Sets Derived? What is Set? What is the meaning of Set in Mathematics? Definition of Sets Example of Sets Rules of Sets in Math Notation of Sets Symbols of Sets What is a Proper Subset of a Set? How can We Describe Sets? Intensional Definition of Extensional

From where the Concept of Sets Derived?

The theory of sets was developed by German mathematician Georg Cantor. He first used the concept of sets in “Problems on Trigonometric Series”.

Today, we use the concept of sets in our day to day life and it is the important branch of mathematics also.

The concept of sets is used to understand the relations and functions.
 

• Set of number of states in a country.

• Set of different wild animals

• Set of clothes

• Set of no. of students in a class
   

What is the meaning of Set in Mathematics?

In mathematics, collection of different things means, group of real numbers, group of integers, group of prime numbers and so on

Let’s see some examples of collection in mathematics:

• All natural numbers less than 10, i.e., 1, 2, 3, 4, 5, 6, 7, 8, 9.

• All prime numbers less than20,i.e., 1, 2, 3, 5, 7, 11, 13, 17.

• Number of vowels in English alphabet, i.e., a, e, i, o, u.
   

Definition of Sets

A SET is a proper or well defined collection of different objects. It could be anything like a set of 10 natural numbers less then 11.So the numbers will be 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10  in this set. Here all the numbers have their own identity if we see them identically but collectively they make a set of natural numbers less than 11.i.e., {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

As in the given picture we can say that it is a collection of shoes, socks and trousers. We can say that trousers belong to this group of clothes but shirt does not belong to it.

Here the curly brackets shows the set and the objects inside it are the elements of a set.
 

Rules of Sets in Math

Notation of Sets

• Objects and elements of a set are one and a same thing.

• Sets are generally written with capital letters like A, Y, Z, etc.

• Elements of a set are written with small letters like a, y, z, etc

• Sets are generally represented by listing each element separated by a comma, and then put curly brackets around it: 

• A = {a, b, c,…}

• The curly brackets { } are also called "braces".

• The three dots here ... are called an ellipsis and it means "continue on".

• In the above picture it is an infinite set.

• These three dots can be used in between also for the long listings.

• Some standard sets used in mathematics are given below;

For Example:

{a,b,…,y,z} It is a definite set as it has 26 English alphabets in it.

• Some standard sets used in mathematics are given below;

  • N: used for the set of all natural numbers (1, 2, 3,…)

  • Z: used for the set of all integers (0,-1, 1,-2, 2,…)

  • Q: used for the set of all rational numbers (1/2, 2/3,…)

  • R: used for the set of real numbers (-∞,…, ∞)

  • W: used for the set of Whole numbers
     

Symbols of Sets

• If b is an object or element of set B, we read it as “b belongs to B”

For which, we use the Greek symbol ∈ (epsilon), which means ‘belongs to’.

Thus, we will write b∈B. If ‘c’ is not an element of set B, we write c∉B and read “c does not belong to B”.

For Example

P ={x: x is the set of prime numbers less than 40}, so 2∈P but 3∉P

• If all the elements of set A are there in a set B than A is the subset of A.We represent it with a symbol ‘⊂’ i.e., Subset.

​For Example

B = {2,4,8}

A = {2,4}

A ⊂ B, as 2 and 4 are there in set B.
 

What is a Proper Subset of a Set?

If all the elements of the set M are included in the elements of set N, then set M is the subset of set N. We denotes subset as M⊂N. 

If all the elements of Set L are included in set N , but all the elements of set N are not included in set L. Then Set L will be the proper subset of set N.

For Example

Set N = {5, 10,15,20}

Set M = {20,15,10,5}

Set L = {10,15}

Set K = {8,10}

Here, 1. M⊂N ,i.e., Set M is the subset of Set N,As all the elements of M are there in N.

2. L is the proper subset of N , as all the elements of L are there in N but all the elements of N are not there in L.

            3.K ⊄N, i.e., Set K is not even a subset of N as 8 is not the element of Set N
 

Let’s see some examples of Sets

Example: What does Set A and Set B represents in the below picture?

Sol. Here,

A = {A, B, C, D, E}

“A” is the set, so it is denoted with capital letter.

A, B, C, D and E are the elements of set A.

The number of elements here are 5, so we will write it as,

n (A) =5

All the elements belong to set A, so we can write as:

A∈A, A belongs to set A

B∈A, B belongs to set A

C∈A, C belongs to set A

D∈A, D belongs to set A

E∈A, E belongs to set A

But, any other thing like “F” does not belong to set A, so we can write it as,

F∉A, F does not belong to set A

Now, if we talk about Set B in above picture,

B = {January, February, March, April, May}

“B” is the set, so it is denoted with capital letter.

January, February, March, April and May are the elements of set B.

The number of elements here are also 5, so we will write it as

n (A) =5

All the elements belong to set B, so we can write as:

January∈B,                 January belongs to set B

February∈A,               February belongs to set B

March∈B,                    March belongs to set B

April∈B,                       April belongs to set B

March∈B,                    May belongs to set B

But, any other month like “December” does not belong to set B so we can write it as,

                        December∉B,    December does not belong to set B

Now,It shows that both the above two sets, Set A and Set B are equivalent sets as their number of elements are same, i.e., 5,

But these are not equal sets, as their elements are not same. A set is called equal sets when their elements are same but are called equivalent sets when their number of elements are same.

How can We Describe Sets?

Sets can be described with two methods or you can say that we can describe the elements of a set in two ways:

 

Intensional (through a rule or semantic description)

Here we just have to give the description of the elements of the sets in a descriptive form. We will not use any braces here.

Example:

X is the set of days which starts with alphabet T.

Y is the set of three colors of the French flag.

Sometimes we use the braces to describe the elements of sets in Intensional definition.

Example:

X = {x: x is the day of the week and x starts with T}

We will read it as “Set X is a set of all the elements x such that x is a day of a week which starts with T letter”.

In this notation, we use the colons “:” which means “such that” and it can be denoted by “I” also, both have the same meaning.

When we write the description of sets in this notation then it is called Set builder form.
 

Definition of Extensional

In this form, we have to list all the elements of the set and then write them in the curly brackets. It is the most common form of representing sets. As it is easy to read and understand. It is also called the Roster or Tabular form.

Example:

T = {Tuesday, Thursday}

S = {Saffron, White, Green}.

Here we had just list the elements and then written them in the curly brackets.

In the above examples,

Set X=Set T and Set Y= Set S

Because the elements of these sets are same.

Some important points to be noted are-

• The element should not be repeated in this form. If you have a set in which there are two same elements, then you will write it only one time.

Example 

F= {25, 25, 30, 30}

• Then you will write it as, F= {25, 30}. The meaning of both the sets will remain same.

The order of the members of a set also does not have any relevance. So, you can write the elements of a set in any Sequence.

As in the above example, you can write it as, F= {30, 25}, Here the meaning will remain same.

So that,

F= {25, 30} = {30, 25} = {25, 25, 30, 30}

At some places, you may see that there are three ways of describing sets i.e., Description form, Roster form and Set builder form.

But basically, there are two major forms i.e., roster form and set builder form, because set builder form is the extension of descriptive form.
 

Let’s see some examples on describing Sets