Reflection of Light by Spherical Mirrors
Table of Content |
|
|
Introductory Concepts
Spherical Mirror
Consider a glass with a hollow sphere and a reflecting surface. This reflecting hollow surface of sphere of which either sides are polished, forms the spherical mirrors. Spherical Mirrors are of two types: (a) Concave Mirror
(b) Convex Mirror
Consider the diagram given below. The inward curved reflecting surface of the spherical mirror as seen in the figure below is known as Concave Mirror and the outward curved reflecting surface of the same spherical mirror is known a Convex Mirror.
Incident Ray, Normal and the Reflected Ray
When a light travels from a point and strikes a reflecting surface making an angle with the normal which is perpendicular to the surface, then the light gets reflected at the same angle that it formed with the normal. The light that is travelling and incident on the surface is known as the Incident Ray and the perpendicular that is drawn to the reflecting surface is known as Normal.The portion of the light that gets reflected is known as the Reflected Ray.
Pole and Optical Centre
The centre of a spherical mirror is known as Pole and the centre of a spherical lens is known as Optical Centre.
Types of Reflection
The reflection of the light depends on the surface of the material it is incident on. Thus reflection can be classified into two types based on the surface:
(a) Regular Reflection: When the surface on which the light is incident is smooth and does not have any irregularities then the reflection is known as Regular Reflection.
(b) Diffused Reflection: When the surface on which the light is incident has deformities, that is, it is not smooth then the reflection is known as Diffused Reflection. Diffused reflection does not help in forming images of the object. For Example, when light falls on paper we do not see any reflection or image formation. This is because the surface of the paper is rougher than the surface of the mirror.
Laws of Reflection
(a) The angle between the incident ray and normal that is, angle of incidence is always equal to the angle between normal and reflected ray that is, angle of reflection
(b)The ray which is incident on the surface, the normal and the ray which is reflected back lies on the same plane
Types of Images
(a) Real Image: When the image is formed on the same side as that of the mirror, then the image is known as Real Image. In other word, if the image can be tossed on the screen, it is a real image.
(b) Virtual image: If the image cannot be tossed on a screen and is formed on the other sides of the mirror by external extension of rays, then the image formed is known as Virtual Image.
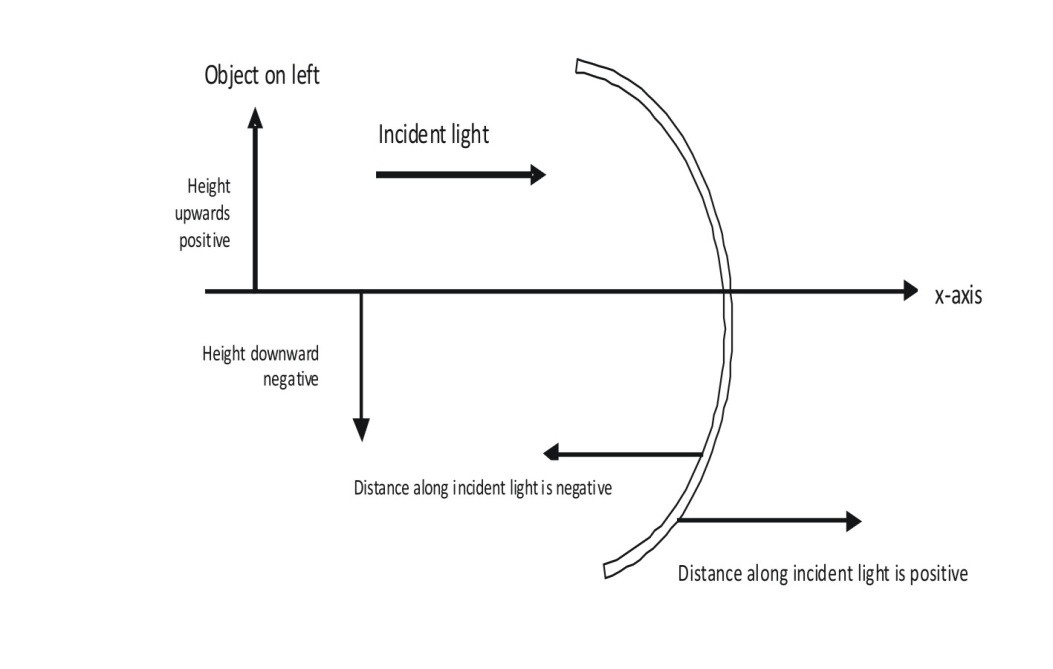
Sign Convention
In order to calculate the distance that help us to derive the relevant formulas for reflection and refraction, we take the help of sign convention.
According to the standard Cartesian sign convention, the pole is the only point from where all the distance will be calculated. The conventions are as follows:
For Distance
Suppose if we want to measure the distance along the same direction of incident light than we consider the value of the distance to be positive. Similarly, if we measure the distance opposite to the direction of incident light, we consider the value of distance to be negative.
For Height
If the height is measured in upward direction perpendicular to principal axis, then the value of height is considered to be positive, while if the height is to be measured in the downward direction perpendicular to the principal axis then, it is considered to be negative. For better understanding consider the diagram below.
Fig: The standard Sign convention (Cartesian)
Focal Length (Spherical Mirrors)
Now we are going to study how when a beam of light is made incident near the pole of a mirror and making small angle(negligible) with it, then the reflected rays converges and diverges for both concave mirror and convex mirror respectively, at some point say F on the principal axis. This point is known as Principal Focus. Now when the light is made incident near the pole, making an angle (not negligible), then the reflected rays appears to converge or diverge from a plane that is perpendicular to principal axis through F. This plane is known as Focal Plane. The distance between the focus and the pole is known as Focal Length (f).
Relation between focus (F) and radius of curvature (R) of a Mirror
Fig: When the light is incident on concave mirror
Fig: When the light is incident on convex mirror
As we can see from the diagram that a beam of light strikes the mirror at point J. Therefore, CJ is perpendicular to the mirror at point J. Since θ is the angle of incidence and JK is perpendicular to the principal axis, therefore,
Now as we have already studied that when the θ is very small that is, negligible it is very close to the pole. Also the distance between the pole and the focus is known as Focal Length(f).
Thus in the diagram FK = f and CK = R(radius of curvature)
∴ f = R/2
The Mirror equation
When a ray of light after travelling from one point of an object gets reflected or refracted to another point, then that point is known as the Image of the Object. If the rays actually appear to converge at a point then the image is said to be real. However, if the rays appear to diverge at point when the rays actually do not meet, when stretched backward, then the image is said to be virtual.
The formation of an image follows some basic principle for tracing the path of the ray. The intersection of the points obtained by tracing the path of the rays is the actual position of the image formed.
The basic principles are as follows:
(a) When the light is travelling parallel to the principal axis, then the reflected ray is supposed to pass through the focus of the mirror
(b) When the light travels through the centre of curvature, then it reflects back and traces its original path that it travelled.
(c) When the light travels through the focus of the mirror, then the reflected rays travels parallel to the principal axis.
It may be noted that these principles abide by the laws of reflection that is, the angle formed by the incident ray is equal to that angle formed by the reflected ray.
Let us consider the diagram given below to obtain the mirror equation:
In the above diagram we consider three rays for time being radiated from the top of the object. We see that the point at which the rays intersect each other, a real image is formed at that point. In this case we have considered a concave mirror. To derive the equation for mirror we have considered the distance between pole and focus of the mirror to be f; the distance between the pole and image formed is ‘v’ and the distance between the pole and the object is ‘u’. Therefore,
∵ ∆ Y’ Z’ F and ∆ FPJ are similar triangles by AAA corollary

From (1) and (2) , L.H.S = L.H.S

The above equation is known as Mirror Equation. Kindly note that we have considered the negative sign because in order to measure the distance we are required to travel opposite in the direction of the incident light.
Formula of Magnification
In simple words, magnification means enlargement of the image. It can also be defined as the ratio of height of the image to height of the object. Consider the diagram given below:

[Here is taken as negative because the image is formed below the principal axis.]

The above equation is known as Magnification Formula for Spherical Mirrors.
If the height of the image is positive then the height of the image is considered to be positive and if the image formed is inverted that is, lying below the principal axis then the height of the image is considered to be negative.
Both the mirror equation and magnification formula is true for Real as well as virtual image.
Examples
Example 1:
Let us consider that an object is placed at 25 cm in front of a concave mirror whose radius of curvature is 10 cm and we are supposed to find the image position, magnification and nature of the image. With the help of mirror equation and magnification formula, we know

Thus, the image formed is inverted and is formed at a distance of – 6.25 cm from the pole, which that the image is real.
Now to calculate the magnification of the image we use the magnification formula:
We know,

Note: The image formed in concave mirror can be real or virtual but in case of convex mirror the image formed is always virtual and erect. Let us consider the example below:
Example 2:
Let us consider that an object is placed in front of a convex mirror at a distance of 40 cm and the radius of curvature of the mirror is 30 cm and we are supposed to find the position of the image as well as its nature and its magnification
A/Q, u= 40 cm, f = 30/2= 15 cm
Applying mirror equation,
Thus, the image is formed 24 cm from the pole behind the mirror.
Applying magnification formula,

Thus, the image formed is diminished and erect.
Frequently Asked Questions (FAQs)
Q1. What do you mean by spherical mirrors?
Sol. The portion of the hollow sphere whose inner or outer area has been polished is known as Spherical Mirrors. Spherical Mirrors are of two types:
-
Concave Mirror (Outer Area Polished)
-
Convex Mirror (Inner Area Polished)
Q2. What are the uses of a concave mirror?
Sol. The uses of concave mirror are as follows:
(a) Used as mirror by dentists
(b) Used in reflecting telescopes
(c) Used as reflector in projectors, headlights of motor cars etc.
Q3. What is a mirror in physics?
Sol. A mirror is a smooth surface material that helps us to capture an image of an object
Q4. Is an image formed by reflection real or virtual? Where is it located?
Sol. The image formed can be real or virtual depending on the size, position and location of the object. For concave mirrors it can be real or virtual, but for convex mirror the image formed is always virtual and erect.
Watch this Video for more reference
More Readings

-and-radius-of-curvature-(-r-)-of-a-mirror.png)






