Refraction at Spherical Surface and by Lenses
Table of contents |
|
|
Basic Concepts
Refraction: The bending of light when it travels from one medium to another is known as Refraction. Normally, when a light travels from a denser medium to a rarer medium, the light changes its direction and moves away from the normal and while travelling from lighter medium to a denser medium it shifts its direction and moves closer to the normal.
Cause of Refraction: The main reason why the light changes its direction while travelling from one medium to another depends on the factor known as Refractive Index of the Material. As the refractive index is different for different medium, thus the speed of the light changes while travelling through them, resulting in the change of direction.
Optically Rarer and Denser Medium: A medium is said to be optically denser, when the speed of the light is more in that medium. Similarly when the speed of a light is less in a medium, it is said to be an optically rarer medium.
Laws of Refraction
(a) The incident ray, the refracted ray and the normal lies in the same plane.
(b) The sine of both the angles, that is, the angle of incidence to the angle of refraction is constant for the two media, the light is travelling through.
The refractive index of a medium can also be understood as the speed of the light in first medium through which the light is travelling to the speed of the light in the second medium, where the light gets refracted. The refractive index of the air is 1.0003.
Refraction by Spherical Lenses
Lens: A lens consists of two transparent glass surfaces on the same side. The portion which is curved inwards is known as Concave Surface and the portion which is bulged outwards is known as Convex Surface. These two together form a lens.
Optical Centre and Principal Axis of a Lens
The central point of a lens is known as Optical centre of Lens. The line passing through the optical centre of the lens is known as Principal Axis. The principal axis is perpendicular to the both concave and convex surface of the lens.
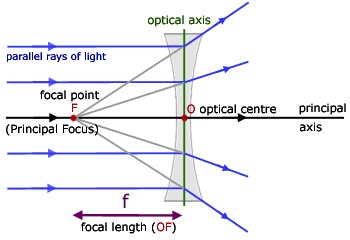
Principal Focus and Focal Length of a Convex Lens: A parallel beam of lights after travelling parallel to the principal axis and passing through the convex surface, converges at a point on the principal axis. This point is known as the Principal Focus. Since a lens has two convex surfaces, thus a lens is said to have two foci. Both the foci of a lens are at equal distances from the optical centre. The word foci is the plural form of Focus .
Principal focus and focal length of a Concave Lens: Principal focus is defined as the point on principal axis from which the light travelling parallel to the principal axis, appears to diverge after passing through the concave lens.
The distance between optical centre and principal focus is known as Focal Length.
Image formation by Lens
In order to determine the nature, position and size of an image formed by the spherical lenses, we need to know the basic rule of the image formation:
The basic rule are as follows:
-
A ray of light travelling parallel to the principal axis from the object after passing through the convex lens gets refracted and converges at the principal focus located on the other side of the lens. In case of concave lens, the ray of light after passing through the lens, diverges from the principal focus.
-
In convex lens a ray of light after travelling through the principal focus, will travel parallel to the principal axis. In case of concave lens, the rays of light from the object appear to meet at the principal focus of the lens and then travels parallel to the principal axis.
-
When a ray of light from the object passes through the optical centre in both concave and convex lens, it will travel through straight without getting deviated.
Sign Convention for Spherical Lenses
-
All the distance is measured from the optical centre of the lens.
-
The distance measured in the direction parallel to the incident light is always taken positive.
-
The distance measured in the opposite direction of the incident light is taken as negative.
-
The distance measured above and perpendicular to the principal axis is considered to be positive.
-
The distance measured below and perpendicular to the principal axis is considered to be negative.
Another new Cartesian sign convention states that the focal length of convex length is positive and that of concave lens is negative.
Formation of Image by a Convex Lens
We will study the formation of image by convex lens when the image is placed at six different positions:
- When the object is placed between optical centre and focus:
The image formed is behind the object, virtual and erect and larger than the object.
This image formation explains the use of a convex lens as magnifying glass. It should be noted that, the smaller the focal length of a lens, the more is its magnifying power. Thus a magnifying glass with smaller focal length is always preferred to magnify the objects.
-
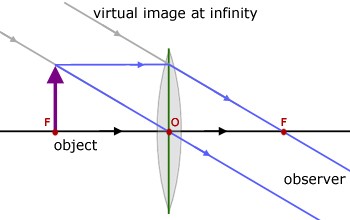
When the object is placed at the focus of a convex lens:
The image formed is at infinity, real and inverted and highly enlarged.
-
When the object is between F and 2F on the left side of the lens:
The image formed is beyond 2F n the right side of the lens, real and inverted and larger than the object.
-
When the object is at 2F:
The image formed is at a distance of 2F on the right side of the lens, real and inverted and of the same size as that of the object
-
When the object is beyond 2F on the left side of the lens:
The image formed is at a distance F and 2F on the right side of the lens, real and inverted and smaller than the object.
-
When the object is at infinity:
The image formed is at the focus, real and inverted and highly diminished.
Similarly, we can find the nature, size and position of image formed in concave lens. The table given below gives the summary of the image formed by both the concave and convex lens:
Image formed by convex lens for different positions of the object
|
Position of the object |
Position of the image |
Size of the image |
Nature of the image |
|
At infinity |
At focus on the right side of the lens |
Highly diminished |
Real and inverted |
|
Beyond 2F on the left side of the lens |
Between F and 2F on the right side of the lens |
Diminished |
Real and inverted |
|
At 2F on the left side |
At 2F on the right side |
Same size |
Real and inverted |
|
Between F and 2F on the left side |
Beyond 2F on the right side |
Enlarged |
Real and inverted |
|
At focus |
At infinity |
Highly enlarged |
Real and inverted |
|
Between focus on the left side and optical centre |
On the same side of the lens as the object |
Enlarged |
Virtual and erect |
Image formed by concave lens for different position of the object.
|
Position of the object |
Size of the image |
Nature of the image |
|
|
At infinity |
At focus F on the left side |
Point sized |
Virtual and erect |
|
Between infinity and optical centre O of the lens |
Between focus and optical centre on the left side |
Diminished |
Virtual and erect |
From the table it can be concluded that whatever be the position of the object, the image formed is always virtual and erect in case of concave lens.
General formula for Lens
The lens formula can be defined as the relation between the image distance, the object distance and the focal length of a lens. Mathematically,
Where v is the image distance, u is the object distance and f is the focal length.
Magnification produced by Lenses
The magnification of the lens can be defined as the ratio of height of the image to the height of the object.
The magnification of lens can also be defined in terms of the ratio of image distance to the object distance.
If the value of magnification (m) is positive then he image formed will be virtual and erect and if the value of magnification is negative, then a real and inverted image is formed. Since we have already seen that a concave lens always produces virtual and erect images, thus the magnification of a concave lens is always positive.
Power of a Lens
The power of a lens is a mathematical term that help us to identify the degree of convergence or divergence of light rays passing through the lens. It can be defined as the reciprocal of focal length of a lens.
Where P is the power and f is the focal length. The S.I unit of Power is dioptre.
The power of a concave lens is negative and that of convex lens is positive.
Power of Combined Lenses
When multiple lenses are placed close to each other, then the power of the combined lens is given by the algebraic sum of the power of an individual lens.
P = P1 + P2 + P3 +………………Pn
Uses of a Concave and Convex Lens
Convex Lens:
-
Concave lens is used to correct hypermetropia (a long sightedness vision defect).
-
They are used in simple cameras
-
They are used as magnifying glass
Concave Lens:
-
It is used to correct myopia (a short – sightedness vision defect).
-
They are used in Galilean telescope.
-
Used as spyholes in doors
-
Optical systems are designed using the combination of both concave and convex lens.
Frequently Asked Question (FAQs)
Q1. How is the power of a lens related to its focal length and what is its use?
Sol. The power of a lens is defined as the reciprocal of the focal length of a lens.
It helps us to define the degree of convergence or divergence of light rays by the lens.
Q2. What is the unit of a power of lens?
Sol. The unit of a power of lens is dioptre.
Q3. Why does a concave lens diverge a rays of light?
Sol. The concave lens diverge the rays of the light because of the fact that the concave lens is thicker at the edges but thinner at the middle. Since we know that when a ray of light travels from denser medium to rarer medium it bends away from the normal. Here the thick edge of the concave lens act as the denser medium, so when light passes through the concave lens, it bends.
Q4. Why does the convex lens converge the rays of light?
Sol. Unlike concave lens, the convex lens is thinner at the edges and thick at the middle. Thus by the same law of refraction, the convex lens converges the ray of light to a single point.
Watch this Video for more reference
More Readings