Refraction at Spherical Surface

Table of Content

Refraction of Light
Cartesian Sign Convention
Cause of Refraction
- Refraction through thin Lenses
- Lens maker’s formula and Lens formula
Refraction at a Spherical Surface
Related Resources

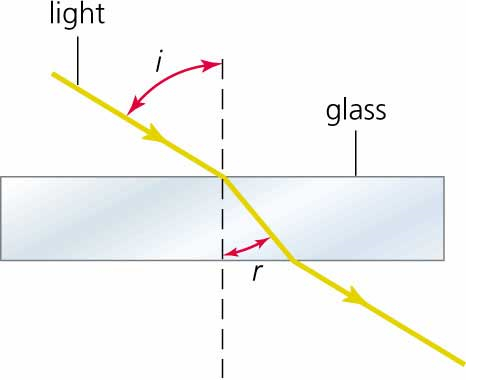Refraction of Light

$Refraction of Light$ When a ray of light travels from one transparent medium into another medium, it bends while crossing the interface, separating the two media. This phenomenon is called refraction.

Image formation by spherical lenses is due to the phenomenon of refraction. The laws of refraction at a plane surface are equally true for refraction at curved surfaces also. While deriving the expressions for refraction at spherical surfaces, we make the following assumptions.

(a) The incident light is assumed to be monochromatic and

(b) The incident pencil of light rays is very narrow and close to the principal axis.

Cartesian Sign Convention

The sign convention followed in the spherical mirror is also applicable to refraction at spherical surface. In addition to this two more sign conventions to be introduced which are:

(a) The power of a converging lens is positive and that of a diverging lens is negative.

(b) The refractive index of a medium is always said to be positive. If two refractions are involved, the difference in their refractive index is also taken as positive.

Cause of Refraction

Refraction is merely one of several possible boundary behaviors by which a light wave could behave when it encounters a new medium or an obstacle in its path. The transmission of light across a boundary between two media is accompanied by a change in both the speed and wavelength of the wave. The light wave not only changes directions at the boundary, it also speeds up or slows down and transforms into a wave with a larger or a shorter wavelength. The only time that a wave can be transmitted across a boundary, change its speed, and still not refract is when the light wave approaches the boundary in a direction that is perpendicular to it. As long as the light wave changes speed and approaches the boundary at an angle, refraction is observed.

Refraction through thin Lenses

$Refraction through thin Lenses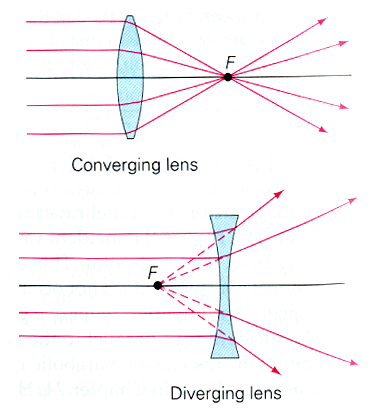$ A lens is one of the most familiar optical devices. A lens is made of a transparent material bounded by two spherical surfaces. If the distance between the surfaces of a lens is very small, then it is a thin lens.

As there are two spherical surfaces, there are two centres of curvature C₁ and C₂ and correspondingly two radii of curvature R₁ and R₂. The line joining C₁ and C₂ is called the principal axis of the lens. The centre P of the thin lens which lies on the principal axis is called the optic centre.

Lens maker’s formula and Lens formula

Let us consider a thin lens made up of a medium of refractive index µ₂ placed in a medium of refractive index µ₁. Let R₁ and R₂ be the radii of curvature of two spherical surfaces ACB and ADB respectively and P be the optic centre.

Consider a point object O on the principal axis. The ray OP falls normally on the spherical surface and goes through the lens un deviated.

The ray OA falls at A very close to P. After refraction at the surface ACB the image is formed at I'. Before it does so, it is again refracted by the surface ADB. Therefore the final image is formed at I as shown in figure.

The general equation for the refraction at a spherical surface is given by

(µ₂/v) – (µ₁/u) = (µ₂ – µ₁/R) …... (1)

For the refracting surface ACB, from equation (1) we write

(µ₂/v ') – (µ₁/u) = (µ₂ – µ₁/R₁) …... (2)

The image I′ acts as a virtual object for the surface ADB and the final image is formed at I. The second refraction takes place when light travels from the medium of refractive index µ₂ to µ₁.

$Refracting surface ADB$ For the refracting surface ADB, from equation (1) and applying sign conventions, we have,

(µ₁/v) – (µ₂/v ') = (µ₂ – µ₁/-R₂) …... (3)

Adding equations (2) and (3), (µ₁/v) – (µ₁/u) = (µ₂ – µ₁) [ 1/R₁ – 1/R₂]

Dividing the above equation by µ₁,

1/v – 1/u = (µ₂/µ₁ – 1) [1/R₁ – 1/R₂] …... (4)

If the object is at infinity, the image is formed at the focus of the lens.

Thus, for u = ∞, v = f. Then the equation (4) becomes.

1/f = (µ₂/µ₁ – 1) [1/R₁ – 1/R₂] …... (5)

If the refractive index of the lens is µ and it is placed in air, µ₂ = µ and µ₁ = µ. So the equation (5) becomes,

…... (6)

This is called the lens maker’s formula, because it tells what curvature will be needed to make a lens of desired focal length. This formula is true for concave lens also.

Comparing equation (4) and (5), we get,

1/v – 1/u = 1/f …... (7)

which is known as the lens formula.

Refraction at a Spherical Surface

$Refraction at a Spherical Surface$ Let us consider a portion of a spherical surface AB separating two media having refracting indices µ₁ and µ₂ as shown in figure. This is symmetrical about an axis passing through the centre C and cuts the surface at P. The point P is called the pole of the surface. Let R be the radius of curvature of the surface.

Consider a point object O on the axis in the first medium. . Consider two rays OP and OD originating from O. The ray OP falls normally on AB and goes into the second medium, un deviated. The ray OD falls at D very close to P. After refraction, it meets at the point I on the axis, where the image is formed. CE is the normal drawn to the point D. Let i and r be the angle of incidence and refraction respectively.

Let ∠DOP = α , ∠DCP = β, ∠DIC = γ

Since D is close to P, the angles α, β and γ are all small. From the figure,

tan α = DP/PO, tan β = DP/PC and tan γ = DP/PI

From the ?ODC, i = α + β …...(1)

From the ?DCI, β = r + γ or r = β − γ …... (2)

From Snell’s Law, µ₁/ µ₂ = sin i/sin r and for small angles of i and r, we can write,

µ₁r = µ₂r …... (3)

From equations (1), (2) and (3)

we get µ₁ (α + β) = µ₂ (β − γ)

or µ₁α + µ₂γ = (µ₂ - µ₁)β …... (4)

Substituting the values of α, β and γ in equation (4)

µ₁ (DP/PO) + µ₂ (DP/PI) = [µ₂ – µ₁] DP/PC

(µ₁/PO) + (µ₂/PI) = (µ₂ – µ₁/PC) …... (5)

As the incident ray comes from left to right, we choose this direction as the positive direction of the axis. Therefore u is negative, whereas v and R are positive substitute PO = –u PI = +v and PC = +R in equation (5),

(µ₁/-u) + (µ₂/v) = (µ₂ – µ₁/R)

…... (6)

Equation (6) represents the general equation for refraction at a spherical surface.

If the first medium is air and the second medium is of refractive index µ, then

(µ/v) – (1/u) = (µ – 1/R) …... (7)

Watch this Video for more reference

The normal line is an imaginary construction line at right angles (perpendicular) to the refracting or reflecting surface at the point of incidence.
When light waves travel into a denser medium the waves are refracted towards the normal and on leaving the denser medium are refracted away from the medium. This is because light travels slower in the denser medium.
When sound waves travel into a denser medium the waves are refracted away from the normal and on leaving the denser medium are refracted towards the medium. This is because sound waves travel faster in a denser medium.
Any incident ray traveling parallel to the principal axis of a converging lens will refract through the lens and travel through the focal point on the opposite side of the lens.
Any incident ray traveling through the focal point on the way to the lens will refract through the lens and travel parallel to the principal axis.
An incident ray that passes through the center of the lens will in effect continue in the same direction that it had when it entered the lens.
Any incident ray traveling parallel to the principal axis of a diverging lens will refract through the lens and travel in line with the focal point (i.e., in a direction such that its extension will pass through the focal point).
Any incident ray traveling towards the focal point on the way to the lens will refract through the lens and travel parallel to the principal axis.
An incident ray that passes through the center of the lens will in effect continue in the same direction that it had when it entered the lens.
The speed of a wave is affected by the medium in which the wave is travelling through or along.
A change in wave speed causes a change in wavelength as the frequency cannot change.

Problem (JEE Advanced):

If the distance of an object and its virtual image from the focus of a convex lens of focal length f are 1 cm each, then f is

(a) 4 cm (b) (√2+1) cm

Solution:

Here, u = – (f – 1)

v = – (f + 1)

f = + f

Applying 1/v – 1/u = 1/f, we have

[1/-(f+1)] + [1/(f –1)] = 1/f

Or, f² – 2f – 1 = 0

This gives f = (√2+1) cm

From the above observation, we conclude that, option (b) is correct.

Problem:

A transparent rod 40 cm long is cut flat at one end and rounded to a hemispherical surface of 12 cm radius at the other end. A small object is embedded with in the rod along its axis and half way between its ends. When viewed from the flat end of the rod, the object appears 12.5 cm deep. What is its apparent depth when viewed from the curved end?

Solution:

For the flat surface:

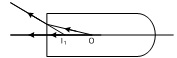Real depth of the object = 20 cm

Apparent depth = 12.5 cm

Using m = real depth / apparent depth

m = 20 / 12.5 = 1.6

For the curved surface:

We will use, (m₁/u) + (m₂/v) = m₂- m₁/R

u = 20 cm, R = -12 cm

So, (1.6/20) + (1/v) = (1 -1.6)/(-12)

Or, 1/v = (1/20) – (1.6/20)

Or, v = -33.3 cm

Hence the object appears 33.3 cm deep from the curved side.

Question 1

A converging lens is used to form an image on a screen. When the lower half of the lens is covered by an opaque screen then,

(a) half of the image will disappear

(b) complete image will be formed

(d) intensity of the image is high

Question 2

Two lenses of power +12 and −2 diopter are placed in contact. The focal length of the combination is given by

(a) 8.33 cm (b) 12.5 cm

Question 3

The bending of a beam of light when it passes obliquely from one medium to another is known as _______.

(a) reflection

(b) refraction

(d) deviation

Question 4

When a person uses a convex lens as a simple magnifying glass, the object must be placed at a distance.

(a) less than one focal length

(b) more than one focal length

(d) more than twice the focal length

Question 5

The image formed by a concave mirror is real, inverted and of the same size as that of the object.The position of the object should be ________.

(a) beyond the center of curvature of mirror

(b) between the center of curvature and the focus

(d) at the focus

Q.1	Q.2	Q.3	Q.4	Q.5
b	d	b	a	c

Related Resources

You might like to polarisation.
For getting an idea of the type of questions asked, refer the Previous Year Question Papers.
Click here to refer the most Useful Books of Physics.
To get answer to any question related to refraction at spherical surface click here.

To read more, Buy study materials of Ray Optics and Optical Instruments comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here.

Live courses Ask question