Polarisation
Table of Content |
The phenomena of reflection, refraction, interference, diffraction are common to both transverse waves and longitudinal waves. But the transverse nature of light waves is demonstrated only by the phenomenon of polarisation, which as shown in the below figure.
Polarisation of Transverse Waves
Let a rope AB be passed through two parallel vertical slits S1 and S2 placed close to each other. The rope is fixed at the end B. If the free end A of the rope is moved up and down perpendicular to its length, transverse waves are generated with vibrations parallel to the slit. These waves pass through both S1 and S2 without any change in their amplitude. But if S2 is made horizontal, the two slits are perpendicular to each other. Now, no vibrations will pass through S2 and amplitude of vibrations will become zero. i.e., the portion S2B is without wave motion as shown in figure.
On the other hand, if longitudinal waves are generated in the rope by moving the rope along forward and backward, the vibrations will pass through S1 and S2 irrespective of their positions.
This implies that the orientation of the slits has no effect on the propagation of the longitudinal waves, but the propagation of the transverse waves, is affected if the slits are not parallel to each other.
A similar phenomenon has been observed in light, when light passes through a tourmaline crystal.
Light from the source is allowed to fall on a tourmaline crystal which is cut parallel to its optic axis.
The emergent light will be slightly coloured due to natural colour of the crystal. When the crystal A is rotated, there is no change in the intensity of the emergent light. Place another crystal B parallel to A in the path of the light. When both the crystals are rotated together, so that their axes are parallel, the intensity of light coming out of B does not change. When the crystal B alone is rotated, the intensity of the emergent light from B gradually decreases. When the axis of B is at right angles to the axis of A, no light emerges from B .
If the crystal B is further rotated, the intensity of the light coming out of B gradually increases and is maximum again when their axis are parallel.
Comparing these observations with the mechanical analogue discussed earlier, it is concluded that the light waves are transverse in nature.
Light waves coming out of tourmaline crystal A have their vibrations in only one direction, perpendicular to the direction of propagation. These waves are said to be polarised. Since the vibrations are restricted to only one plane parallel to the axis of the crystal, the light is said to be plane polarised. The phenomenon of restricting the vibrations into a particular plane is known as polarisation.
Plane of Vibration and Plane of Polarisation
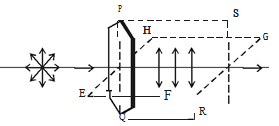The plane containing the optic axis in which the vibrations occur is known as plane of vibration. The plane which is at right angles to the plane of vibration and which contains the direction of propagation of the polarised light is known as the plane of polarisation. Plane of polarisation does not contain vibrations in it.
In the Fig 5.26 PQRS represents the plane of vibration and EFGH represents the plane of polarisation.
Representation of Light Vibrations
In an unpolarised light, the vibrations in all directions may be supposed to be made up of two mutually perpendicular vibrations. These are represented by double arrows and dots.The vibrations in the plane of the paper are represented by double arrows, while the vibrations perpendicular to the plane of the paper are represented by dots.
Polarisation by Reflection
The simplest method of producing plane polarised light is by reflection. Malus, discovered that when a beam of ordinary light is reflected from the surface of transparent medium like glass or water, it gets 
polarised. The degree of polarisation varies with angle of incidence.
Consider a beam of unpolarised light AB, incident at any angle on the reflecting glass surface XY.
Vibrations in AB which are parallel to the plane of the diagram are shown by arrows. The vibrations which are perpendicular to the plane of the diagram and parallel to the reflecting surface as shown by dots.
A part of the light is reflected along BC, and the rest is refracted along BD. On examining the reflected beam with an analyser, it is found that the ray is partially plane polarised.
When the light is allowed to be incident at a particular angle, (for glass it is 57.5o) the reflected beam is completely plane polarised. The angle of incidence at which the reflected beam is completely plane polarised is called the polarising angle (ip).
Brewster’s Law
Sir David Brewster conducted a series of experiments with different reflectors and found a simple relation between the angle of polarisation and the refractive index of the medium. It has been observed experimentally that the reflected and refracted rays are at right angles to each other, when the light is incident at polarising angle.
From Fig, ip + 90° + r = 180º
r = 90° – ip
From Snell’s law, sin ip / sin r = μ
Here μ is the refractive index of the medium (glass)
Substituting for r, we get,
sin ip / sin (90° – ip) = μ
So, sin ip / cos ip = μ
Thus,
The tangent of the polarising angle is numerically equal to the refractive index of the medium.
Watch this Video for more reference
Double Refraction
Bartholinus discovered that when a ray of unpolarised light is incident on a calcite crystal, two refracted rays are produced. This phenomenon is called double refraction as shown in figure (a). Hence, two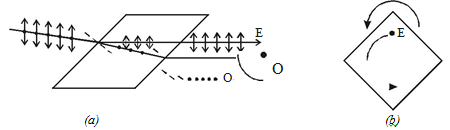 
images of a single object are formed. This phenomenon is exhibited by several other crystals like quartz, mica etc.
When an ink dot on a sheet of paper is viewed through a calcite crystal, two images will be seen in figure. On rotating the crystal, one image remains stationary, while the other rotates around the first. The stationary image is known as the ordinary image (O), produced by the refracted rays which obey the laws of refraction. These rays are known as ordinary rays. The other image is extraordinary image (E), produced by the refracted rays which do not obey the laws of refraction. These rays are known as extraordinary rays.
Inside a double refracting crystal the ordinary ray travels with same velocity in all directions and the extra ordinary ray travels with different velocities along different directions.
A point source inside a refracting crystal produces spherical wavefront corresponding to ordinary ray and elliptical wavefront corresponding to extraordinary ray.
Inside the crystal there is a particular direction in which both the rays travel with same velocity. This direction is called optic axis. The refractive index is same for both rays and there is no double refraction along this direction.
|
|
Problem (JEE Advanced):
In a double slit experiment, the fringes are displaced by a distance x when a glass plate of refracted index 1.5 is introduced in the path of one of the beams. When this plate is replaced by another plate of same thickness, the shift of fringes is (3/2) x. The refractive index of second plate is
(a) 1.75 (b) 1.40
(c) 1.25 (d) 1.67
Solution:
We know that, shift = (μ – 1)tD/d …... (1)
x = (1.5 – 1)tD/d
and (3/2) x = (μ – 1)tD/d …... (2)
Dividing equation (1) by equation (2) we get,
2/3 = 0.5/(μ – 1)
2μ – 2 = 1.5
2μ = 3.5
Or, μ = 1.75
Thus, from the above observation we conclude that, the refractive index of second plate would be 1.75. Therefore option (a) is correct.
Question 1
In appearance of colour in thin films is due to
(a) diffraction (b) dispersion
(c) interference (d) polarization
Question 2
The blue colour of the sky is due to
(a) diffraction (b) reflection
(c) polarization (d) scattering
Question 3
What principle is responsible for the fact that certain sunglasses can reduce glare from reflected
surfaces?
(a) refraction
(b) polarization
(c) diffraction
(d) total internal reflection
Question 4
The principle which allows a rainbow to form is
(a) refraction
(b) polarization
(c) dispersion
(d) total internal reflection
Question 5
When a light wave enters into a medium of different optical density,
(a) its speed and frequency change.
(b) its speed and wavelength change.
(c) its frequency and wavelength change.
(d) its speed, frequency, and wavelength change.
| Q.1 | Q.2 | Q.3 | Q.4 | Q.5 |
|
c |
d |
b |
c |
b |
Related Resources
-
You might like to interference by thin film.
-
For getting an idea of the type of questions asked, refer the Previous Year Question Papers.
-
Click here to refer the most Useful Books of Physics.
-
To get answer to any question related to polarisation click here.