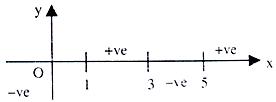Functions: One-One/Many-One/Into/Onto
Functions can be classified according to their images and pre-images relationships. Consider the function x → f(x) = y with the domain A and co-domain B.
If for each x ε A there exist only one image y ε B and each y ε B has a unique pre-image x ε A (i.e. no two elements of A have the same image in B), then f is said to be one-one function. Otherwise f is many-to-one function.
e.g. x → x3, x ε R is one-one function
while x → x2, x ε R is many-to-one function. (see figure above)
e.g. x = + 2, y = x2 = 4
Graphically, if a line parallel to x axis cuts the graph of f(x) at more than one point then f(x) is many-to-one function and if a line parallel to y-axis cuts the graph at more than one place, then it is not a function.
For a one-to-one function
If x1 ≠ x2 then f(x1) ≠ f(x2)
or if (x1) = f(x2) => x1 = x2
One-to-one mapping is called injection (or injective).
Mapping (when a function is represented using Venn-diagrams then it is called mapping), defined between sets X and Y such that Y has at least one element 'y' which is not the f-image of X are called into mappings.
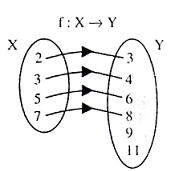
Let a function be defined as: f : X → Y
Where X = {2, 3, 5, 7} and Y = {3, 4, 6, 8, 9, 11}
The mapping is shown in the figure below.
Clearly, element 9 and 11 of Y are not the f-image of any of x ε X
So the mapping is into-mapping
Hence for into mappings:
f[X} 
Y and f[X] ≠ Y. => f [X] 
Y that is range is not a proper subset of co-domain.
The mapping of 'f' is said to be onto if every element of Y is the f-image of at least one element of X. Onto mapping are also called surjection.
One-one and onto mapping are called bijection.
Illustration
Check whether y = f(x) = x3; f : R → R is one-one/many-one/into/onto function.
We are given domain and co-domain of 'f' as a set of real numbers.
For one-one function:
Let x1, x2 ε Df and f(x1) = f(x2)
=>X13 =X23
=> x1 = x2
i.e. f is one-one (injective) function.
For onto-into:
Ltx→a y = Ltx→a (x)3 = α
Ltx→a y = Ltx→a (X)3 = -α
Therefore y = x3 is bijective function.
Illustration:
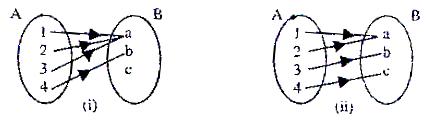
What kind of function does the Venn diagram in figure given below represent?
Solution: This many-one into function
Domain = Df = {a, b, c}
Co-domain = {1, 2, 3}
Range = Rf = {1, 2}
f(a) = 1 ; f(b) = 2; f(c) = 2
Examples
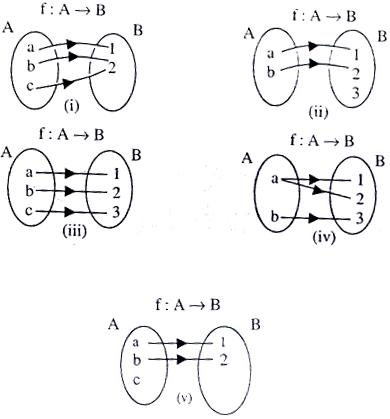
Classify the following functions.
Ans.
(i) Many-one and onto (surjective).
(ii) One-one (injective) and into.
(iii) One-one (injective) and onto (surjective) i.e. Bijective.
(iv) and (v) are not functions.
Examples:
1. Given the sets A = {1, 2, 3, 4} and B = {a, b, c} construct a
(i) Many-one into
(ii) Many-one onto function
2. Given the sets c = {1, 2, 3} and D = {a, b, c}
(i) How many one-one onto functions can be constructed.
(ii) How many-one into functions can be constructed.
Ans.1
f : A → B f : A → B
2. (i) 6
(ii) 33 - 6 = 21
Illustration:
What is the domain and range of the following functions?
(a) y = 3x + 5 (b) y = (x2 +x)/(x2 - x)
Domain of y = f(x) is the set of values of x for which y is real and finite.
Range is the set of values of y for which x is real and finite.
Solution:
(a) For all real and finite x, y is also real and finite
Therefore Df = R = (-∞, ∞) and Rf = R = (-∞,∞)
(b) y = (x(x+1))/(x(x-1)) = (x+1)/(x-1) , x ≠ 0
when x = 0, y is 0/0 from (i.e. indetermined form)
when x = 1, y = ∞ (infinite)
Therefore Df = R -{0, 1}
also xy - y = x + 1
=> x (y - 1) = y + 1
x = (y+1)/(y-1)
when y = 1, x = ∞ (infinite) => y ≠ 1
also, for ≠ 0 => y ≠ -1
Therefore Rf = R - {-1, 1}
Illustration:
What is the domain of the following functions?
(a) y =√((x-1)(3-x)) (b) √(((x-1)(x-5))/(x-3)) (c) y = √sin x
Solution:
(a) y is real and finite if (x - 1)(3 - x) > 0
or (x - 1)(x - 3) < 0
i.e. x - 1 < 0 and x - 3 > 0 or x - 1 > 0 and x - 3 < 0
=> x < 1 and x > 3 => 1 < x < 3
which is not possible => 1 < x < 3
=> Df = [1, 3]
(b) Numerator becomes zero for x = 1, x = 5
Denominator becomes zero for x = 3
These three points divide x-axes into four intervals
(-∞, 1), (1, 3), (3, 5), (5, ∞)
Therefore Df = [1, 3) υ [5, ∞); at x = 3, we here open interval,
Because at x = 3, y is infinite.
(c) y = √sin x
sin x > 0 ∀ x ε [2n∏, (2n + 1) ∏], n ε I
Examples:
1. What is domain of the following?
(a) y =√((x-1)(3-x)) (b) y = √xsinx (c) y = Sin-1((1+x2)/(2x))
2. What is domain and range of the following?
(a)
(b) y =|x
Ans.
1. (a) Df = [1, 3)
(b) Df = [-(2n-1)∏, -2(n-1)∏] υ [2n ∏, (2n + 1)∏], n ε N
(c) Df = {-1, 1}
2. (a) Df = [a, b[ and Rf = [c, d]
(b) Df = {0, 1, 2, 3, 4,......}
Rf = {1, 2, 6, 24, ......}
AskIITians is unique platform which offers you one year and two years online classroom programmes for IIT JEE, AIEEE and other engineering examinations. You can be a part of these programmes even from home and for that you need not travel down to any other place.
To read more, Buy study materials of Set Relations and Functions comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.