Composite Functions

 

Another useful combination of two functions f and g is the composition of these two functions. Let f : X → Y and g : Y → Z be two functions.

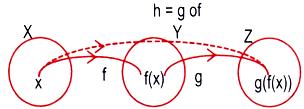
We define a function h : X → Z by setting h(x) = g(f(x). To obtain h(x), we first take the f-image f(x), of an element x in X so that f(x) ε Y, which is the domain of g(x) and then take the g-image of f(x), that is, g(f(x)), which is an element of Z. The scheme is shown in the figure.

The function h, defined above, is called the composition of f and g and is written gof. Thus (gof)(x) = g(f(x)). Domain of gof = {x : x in domain f, f(x) in domain g}.

e.g. Let f : R → R be a function defined by f(x) = x² + 4 and g[0, ∞) → R be a function defined by g(x) = √x. Then gof(x) = g(f(x)) = √(x² + 4). Domain of gof = R. Thus we have gof : R → R defined by (gof)(x) = √(x² + 4). Similarly, we shall have fog : [0, ∞) → R defined by (fog)(x) = x + 4. Note that (gof)(x) ≠ (fog)(x).

Illustration: Two functions are defined as under:

             

Find fog and gof.

Solution: (fog)(x) = f(g(x))  

Let us consider, g(x) < 1 :

(i) x² < 1, -1 < x < 2  =>  -1 < x < 1, -1 < x < 2 => -1 < x < 1

(ii) x² + 2 < 1, 2 < x < 3  =>  x < -1, 2 < x < 3 => x = φ

Let us consider, 1 <  g(x)  <  2,

(iii) 1 < x² < 2,  -1 < x < 2

=> x ε [-√2, -1) υ (1,√2] ,  -1 < x < 2  =>  1 < x < √2

(iv) 1 < x+2 < 2, 2 < x < 3 => -1 < x < 0, 2 < x < 3, x = φ

   

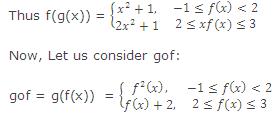
Let us consider -1 < f(x) < 2 :

(i)     -1 < x+1 < 2, x < 1 => -2 < x < 1, x < 1 => -2 < x < 1

(ii)    -1 < 2x+1 < 2, 1 < x < 2 => -1 , x < ½, 1 < x < 2 => x= φ

Let us consider 2 < f(x) < 3:

(iii)    2 < x+1 < 3 ,  x < 1 => x < 2 , x < 1 => x = 1

(iv)   2 < 2x+1 < 3, 1 < x < 2 => 1 < 2x < 2, 1 < x < 2

=> ½  <  x  <  1 , 1 < x < 2 => x = φ

If we like we can also write g(f(x)) = (x+1)2, -2 < x < 1.

To read more, Buy study materials of Set Relations and Functions comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.