Cartesian Product of Sets
Table of Content |
Define Sets
In Mathematics, sets are the most fundamental concepts. It is defined as the collection of well defined and distinct objects of particular kind. The objects which belong to a set are called its Elements. These elements can be of any type for example people, colours, numbers, toys and so.
Few examples of sets:
-
Set of odd/even/natural/whole/prime numbers
-
Set of colours of rainbow
-
Set of Indian rivers
-
Set of applications in a mobile
Sets can be represented either in Roster form or Set builder form.
Above figure is a set of polygons have number of sides less eight.
What is the cardinality of a set?
Cardinality for any set represents the number of elements present in that particular set. For a set A, it is represented by n(A)
For Example
For a set A = {1, 3, 5, 7, 9}, cardinality for set A = n(A) = 5.
Depending upon the cardinality or the number of elements present, the sets are classified as finite or infinite set.
In case of finite set, the number of elements or its cardinality is finite. Set of colours of rainbow, set of playing cards, set of output of a dices are the examples of finite set.
Infinite sets have infinite number of elements in its set. Its examples are – set of natural numbers, set of all the points on a plane.
A set which is not finite is called as Infinite Set and Vice Versa.
What do you mean by ordered pair of sets?
If we have two sets A and B, then (a, b) where a ∈ A & b ∈ B is called as the Ordered Pair. Moreover (a, b) ≠ (b, a) in all the cases. This means, for the two sets A and B, depending upon the situation or requirement, we choose one of the sets as a primary set whose elements are treated as the first elements while the other will be secondary set whose elements are called as the second elements. Thus, if Set A is primary and Set B is secondary that is, relation or mapping is from A to B, then corresponding ordered pairs will be of the form (a, b), such that a ∈ A & b ∈ B.
Ordered pairs are used in Cartesian product, relations and functions. We shall learn this with the examples in next section.
Equality of ordered pairs
Two ordered pairs (a1, b1) and (a2, b2) are said to be equal if a1 = a2 & b1 = b2
Find the values of a and b if
(3a – 2, b + 3) = (2a – 1, 3)
b + 3 = 3, 3a – 2 = 2a – 1
a = 1, b = 0
Explain Cartesian Product of Sets
Cartesian Product of the two sets is defined as the collection or set of all the possible ordered pairs between the two sets in proper order or sequence. Cartesian product of two sets A and B is denoted by A X B or B X A. Both A X B & B X A are different and accordingly the ordered pairs will be (a, b) or (b, a) respectively.
For Example
Let Set A = {1, 2, 3} and set B = {x, y}
Then Cartesian product of A and B that is, A X B = {(1, x), (1, y), (2, x), (2, y), (3, x), (3, y)}
While B X A = {(x, 1), (x, 2), (x, 3), (y, 1), (y, 2), (y, 3)}
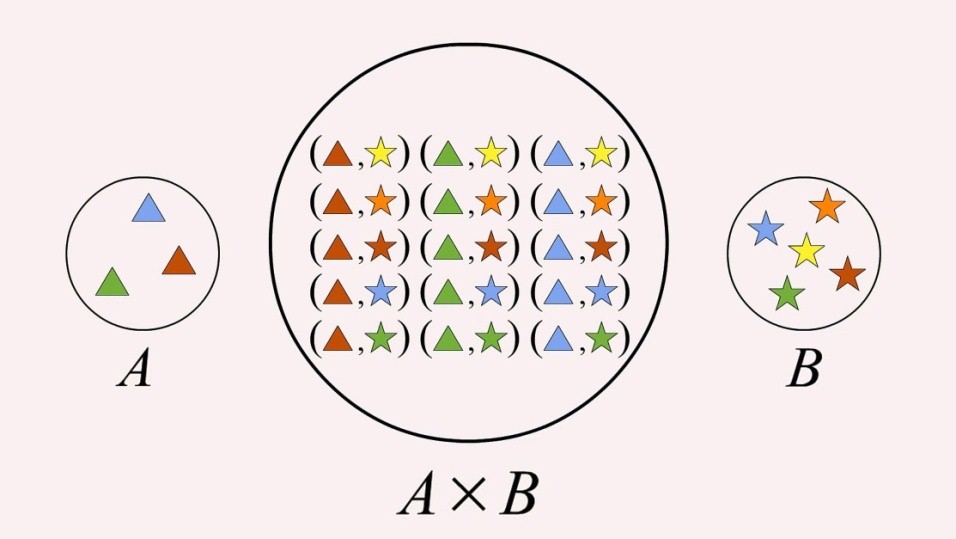
See the below image for another example on Cartesian product.
 |
 |
What are Relations in mathematics?
Understanding relations requires basic knowledge of sets. A Set is a collection of well defined objects of particular kind. For Example, a set of outcomes of dice, a sets of English alphabet.
Relation is always studied between two sets. If we have two non empty sets A and B then the relation R from set A to set B is represented by aRb, where a and b are the elements of the sets A and B respectively.
Relation from a set A to a set B is the subset of the Cartesian product of A and B i.e. subset of A x B. Relation can also be defined as an collection of ordered pairs (a, b) where a belongs to the elements from set A and b from set B and the relation is from A to B but not vice versa.
For Example
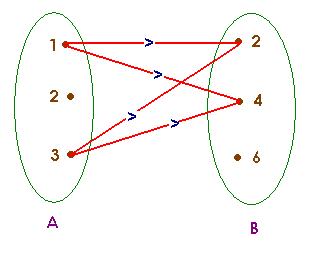
Consider a set A containing elements as {1, 2, 3} and set B contains elements as {2, 4, 6}.
Then the relation between Set A and B from A to B will be set of any combinations from Set A to set B.
From the above diagram, we can see that Relation from A to B i.e. R will be set of {(1,2). (1,4), (3,2), (3,4)}. This relation is a subset of the Cartesian product of two sets A X B.
Let’s take another example where, set A = {1, 2, 3} and set B = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
If the Relation between A and B is as: elements of B is the squares of elements of set A, then the relation is written in the form of sets as:
R = {(a,b): where b is square of a and a ∈ A & b ∈ B}
Then R = {(1,1), (2,4), (3,9)}
Same as sets, relation may also be represented algebraically either by the Roster method or by the Set-builder method.
Relation can also be defined as a linear operation which establishes relationship between the element’s of two set’s according to some definite rule of relationship.
R: {(a,b) | (a,b) ∈ A x B and a R b}
Example
A is {2, 3, 5}
B is {1, 4, 9, 25, 30}
If a R b →b is square of a
Discreet element of relation are {(2,4), (3,9).(5, 25)}
Example
A = {Jaipur, Lucknow, Bhopal}
B = {Rajasthan, Uttar pradesh, Madhya Pradesh}
aRb → a is capital of b,
A X B = {(Jaipur, Rajasthan), (Lucknow, Uttar Pradseh), (Bhopal, Madhya Pradesh}
Total Number of Relation from A to B
Let the number of relations from A to B be x.
Let A contain ‘m’ elements and B contains ‘n’ elements,
Number of element’s in A x B m x n
Number of non void subset’s = C1mn+ C2mn + …….. + Cmnmn = 2mn - 1.
Thus, for A = {1, 2, 3) & B = {x, y, z}
Number of non void subset’s or the number of possible relations =29- 1 = 511
More Readings