Definite Integral as Limit of a Sum

Table of Content

Introduction to Definite Integral as LImit of a Sum
Methods to express the infinite series as Definite Integral
Differentitation under the Integral Sign
Fundamental theorem of Calculus ( Newton-Leibnitz Formula)
Related Resources

Introduction to Definite Integral as LImit of a Sum

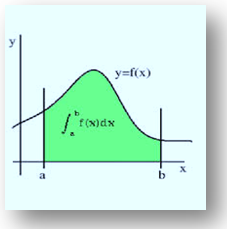
We have already discussed the concept of definite integral in the previous sections. Definite integral is closely related to concepts like antiderivative and indefinite integrals. In this section, we shall discuss this relationship in detail.

Definite integral consists of a function f(x) which is continuous in a closed interval [a, b] and the meaning of definite integral is assumed to be in context of area covered by the function f from (say) ‘a’ to ‘b’.

An alternative way of describing $\int_{a}^{b}f(x)dx$ is that the definite integral $\int_{a}^{b}f(x)dx$ is a limiting case of the summation of an infinite series, provided f(x) is continuous on [a, b] i.e.,

$\int_{a}^{b}f(x)dx = lim_{n\rightarrow \infty} h\sum_{r=0}^{n-1}f(a+rh), where h = (b-a)/n$

The converse is also true i.e., if we have an infinite series of the above form, it can be expressed as a definite integral.

Methods to express the infinite series as Definite Integral

Express the given series in the form ∑ 1/n f (r/n)
Then the limit is its sum when n→∞, i.e. lim _n→∞ h ∑1/n f(r/n)
Replace r/n by x and 1/n by dx and lim_n→∞ ∑ by the sign of ∫.
The lower and the upper limit of integration are the limiting values of r/n for the first and the last term of r respectively.

Some particular cases of the above are

lim n→∞ ∑ⁿ_{r =1} 1/n f(r/n) or lim _n→∞ ∑^n–1_{r = 0} 1/n f(r/n) = ∫¹₀ f(x)dx

lim n→∞ ∑^pn_{r =1} 1/n f(r/n) = ∫^β_α f(x)dx

where α = lim _n→∞ r/n = 0 (as r = 1) and β = lim _n→∞ r/n = p (as r = pn)

Illustration 1:

Show that (A) lim _n→∞ {1/(n+1) + 1/(n+2) + 1/(n+3) + ... + ... 1/(n+n)} = ln 2.

(B) lim _n→∞ 1p + 2p + 3p + ... + np/(np +1) = 1/(p +1) (p > 0)

Solution:

(A) Let I = lim n→∞ (1/n+1 + 1/n+2 + 1/n+3 + ... + 1/n+n)

= lim n→∞ {1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(n+n)}

$= lim_{n\rightarrow \infty} 1/n \sum_{r=1}^{n}1/(1+r/n)$

Now α = lim n→∞ 1/n = 0 (as r = 1)

and β = lim n→∞ r/n = 1 (as r = n)

⇒ l = ∫10. 1/1+x dx = [In (1+x)] 10

⇒ I = ln 2.

(B) 1p + 2p + 3p + ... + np/(np +1) = ∑nr=1 1p/n.np = ∑nr=1 1+n(r/n)p

Take f(x) = xp; Let h = 1/n so that as n → ∞; h → 0

∴ limn→∞ ∑nr =1 1/n f(0 + r/n)

= ∫10 f(x)dx = ∫10 xpdx

= 1/p+1

Differentitation under the Integral Sign

Leibnitz’s Rule

If g is continuous on [a, b] and f₁ (x) and f₂ (x) are differentiable functions whose values lie in [a, b], then

d/dx ∫ f₂(x) f₁(x) g(t)dt = g (f₂(x)) f₂'(x) – g (f₁(x)) f₁'(x)

Illustration 1:

$If f(x) = cos x - \int_{0}^{x} (x-t), then show that {f}''(x) + f(x) = - cos x$

Solution:

f ‘(x) = – sin x – (x f (x) + ∫^x₀ f(t) dt) + x f(x)

= –sin x – ∫^x₀ f(t)dt

f “(x) = – cos x – f(x)

Hence, this gives f “(x) + f(x) = cos x.

____________________________________________________________________________

Illustration 2:

If a function f(x) is defined ∀x ∈ R such that

$g(x) = \int_{x}^{a}f(t)/t dt, then prove that \int_{0}^{a}g(x) dx = \int_{0}^{a}f(x) dx.$

Solution:

$g(x) = \int_{x}^{a}f(t)/t dt$

Diffrentiate w.r.t. x

g’(x) = – F(x)/x

F(x) = -x g’(x)

$\int_{0}^{a}f(x)dx = - \int_{0}^{a}x {g}'(x)dx$

NOw, we know that g(a) = 0 and hence we get

$\int_{0}^{a}f(x) dx = -ag(a) + \int_{0}^{a}g(x) dx = \int_{0}^{a}g(x) dx$

$Hence, \int_{0}^{a}g(x) dx = \int_{0}^{a}f(x) dx.$

______________________________________________________________________________

Illustration 3:

Determine a positive integer n < 5, such that

$\int_{0}^{1}e^{x} (x-1)^{n} dx = 16 - 6e$

Solution:

$Let I_{n} = \int_{0}^{1}e^{x} (x-1)^{n} dx$

Integrating by parts,

$\left [e^{x}(x-1)^{n} \right ]^{1}_{0} - \int_{0}^{1}e^{x}n(x-1)dx = (-1)^{n}dx$

$I_{n} = \left [e^{x}(x-1)^{n} \right ]^{1}_{0} - \int_{0}^{1}e^{x}n(x-1)dx = (-1)^{n+1} = nI_{n-1}$ …... (1)

$Also, I_{1} = \int_{0}^{1}e^{x}n(x-1)^{n-1}dx = \left [((x-1)e^{x}) \right ]^{1}_{0}- \int_{0}^{1}e^{x}ex 1 dx$

= – (–1) – [e^x]¹₀ = 1 – (e–1) = 2 – e

From (i), I₂ = ( -1)³ - 2I₁ = -1 - 2(2 - e) = -5 + 2e

and I₃ = (-1)⁴ - 3I₂ = 1 - 3(-5 + 2e) = 16 - 6e Which is given .

∴ n = 3.

Fundamental theorem of Calculus ( Newton-Leibnitz Formula)

Antiderivative Concept with the Area Problem

This theorem state that If f(x) is a continuous function on [a, b] and F(x) is any anti derivative of f(x) on [a, b] i.e. F'(x) = f (x) ∀ x ∈ (a, b), then $\int_{a}^{b}f(x) dx = F(b) - F(a)$

The function F(x) is the integral of f(x) and a and b are the lower and the upper limits of integration.

Illustration 1:

$Evaluate \int_{-2}^{2}dx/(4+x^{2})$

directly as well as by substitution x = 1/t. Evaluate why the answers don't tally.

Solution:

$I = \int_{-2}^{2}dx/(4+x^{2})$

= [1/2 tan^–1 (x/2)]²_–2 = 1/2 [tan^–1(1) – tan^–1 (–1)]

= 1/2 [π/4 – (–π/4)] = π/4

⇒ l = π/4

On the other hand; if x = 1/t then,

$I = \int_{-2}^{2}dx/(4+x^{2})$

Solving this and simplifying, we get

I = – [1/2 tan^–1 (2t)]^1/2_–1/2

= –1/2 tan^–11 – (–1/2 tan^–1 (–1)) = –π/8 – π/8 = –π/4

∴ I = π/4 when x = 1/t

In above two results l = -π/4 is wrong. Since the integrand ¼ + x² > 0 and therefore the definite integral of this function cannot be negative.

Since x = 1/t is discontinuous at t = 0, the substitution is not valid (∴ I = π/4).

Note:

It is important the substitution must be continuous in the interval of integration.

________________________________________________________________________________________

Illustration 2:

$Let \alpha = \int_{0}^{\infty}dx/(x^{4}+ 7x^{2}+1) and \beta = \int_{0}^{\infty}x^{2}dx/(x^{4}+ 7x^{2}+1)$

then show that α = β.

Solution:

$\alpha = \int_{0}^{\infty}dx/(x^{4}+7x^{2}+1)$

Put x = 1/t ⇒ dx = –1/t² then

$\alpha = \int_{0}^{\infty}-1/t^{2}dt/ (1/t^{4} + 7/t^{2} + 1)$

= $= \int_{0}^{\infty} dt. t^{2}/ (t^{4} + 7t^{2} + 1) = \int_{0}^{\infty}t^{2} dt/ (t^{4} + 7t^{2} + 1) = \beta .$

Q1. The Leibnitz’s rule can be applied only if

(a) the function g is continuous in [a, b] and the functions f₁ and f₂ are differentiable functions whose values may lie within or outside [a, b].

(b) the function g is continuous in [a, b] and the functions f₁ and f₂ are differentiable functions whose values lie outside [a, b].

(c) the function g is continuous in [a, b] and the functions f₁ and f₂ are differentiable functions whose values lie in [a, b].

(d) the function g is discontinuous in [a, b] and the functions f₁ and f₂ are differentiable functions whose values may lie withing or outside [a, b].

Q2. Fundamental theorem of calculus states that $\int_{a}^{b}f(x)dx$ = F(b) – F(a), where

(a) f(x) is a continuous function on [a,b] and F(x) is the derivative of f(x) on [a, b].

(b) f(x) is a continuous function on [a,b] and F(x) is the anti derivative of f(x) on [a, b].

(d) F(x) is a continuous function on [a,b] and f(x) is the derivative of f(x) on [a, b].

Q3. In order to express infinite series as definite integral,

(a) sign of summation is replaced by integration.

(a) sign of integration is replaced by summation.

(a) infinite series can’t be expressed as definite integral.

(a) None of the above.

Q4. The definite integral $\int_{a}^{b}f(x)dx$ is a limiting case of

(a) infinite series

(b) finite series

(d) indefinite integral.

Q5. $lim _{n\rightarrow \infty} \sum_{r=0}^{n-1}1/n f(r/n) =$

(a) $\int_{0}^{2}f(x)dx$

(b) $\int_{1}^{0}f(x)dx$

(d) $\int_{0}^{1}f(x)dx$

Q1	Q2	Q3	Q4	Q5
(c)	(b)	(a)	(a)	(d)

Related Resources

You may wish to refer indefinite integral.
Click here to refer the most Useful Books of Mathematics.
For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Definite integral comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.