IIT JEE Coordinate Geometry- Preparation Tips

 

Table of Content

Important topics in coordinate geometry for IIT JEE Important Concepts and Formulae Distance Formula Section Formula Area of Triangle Equation of Straight Line Distance of a Point from a Line Distance between two Parallel Lines Concurrency of Lines Collinearity of Points Angle between two Lines Position of point w.r.t Line Locus Conic Section Recognition of Conics Eccentricity Circle Parabola Ellipse Hyperbola Some Interseting Facts Books to Refer Tips to Study Coordinate Geometry Practical Application of Coordinate Geometry

Important topics in coordinate geometry for IIT JEE

It is an important topic and can be further divided into important parts like:

2D Geometry	Distance formula
	Section formula
	Area of triangle
	Locus of a point
	Transformation of axis
Straight Lines	Concepts of straight line
Conic Section	Circle
	Parabola
	Ellipse
	Hyperbola
	Pair of straight lines

We shall give a brief introduction of each of these sub – topics along with the tips to master them. Beginners are advised to refer the study material on coordinate geometry.

Important Concepts and Formulae

Distance Formula

Distance ‘d’ between any two points A (x₁,y₁) and B (x₂,y₂) on the coordinate axis is given by

 

Section Formula

Coordinates of P when it divides the line AB in the ratio m : n

       

Area of Triangle

There are many formulas for area of triangle. Basically it depend on what we have given in the question.

•  Case I: If height ‘h’ and base ‘b’ are given. Then area ‘A’ is

 

• Case II: If coordinates of points are given. Let say A(x₁, y₁), B(x₂,y₂ ) and C(x₃,y₃ ). Then area ‘A’ is

Equation of Straight Line

• Case I: Point – Slope form

           Let ‘m’ be the slope of line and line is passing through point A(x₁,y₁). Then equation of line is

• Case II: Point – Point form

          Let line passing through points A(x₁,y₁) and B(x₂,y₂). Then equation of line is

• Case III: Slope intercept form

          Let the slope of line be ‘m’ and intercept it made on y-axis is ‘c’. Then equation of line is

• Case IV: Intercept form

          Let the line made an intercept ‘a’ and ‘b’ on x-axis and y-axis respectively. Then equation of line is

• Case V: Normal form

          Let the distance of line from the origin is ‘p’ and the angle it made with the origin is .Then equation of line is

Distance of a Point from a Line

Line:ax+by+c=0. Let the point be P(x₁,y₁). Then distance ‘d’ of the point P from the line is

Distance between two Parallel Lines

Line 1: ax+by+c=0, Line 2: ax+by+c^’=0.Then distance ‘d’ between lines is

Concurrency of Lines

Two lines are always concurrent if they are not parallel. Three lines

Line 1: a₁x+b₁y+c₁=0 ,  Line 2: a₂x+b₂y+c₂=0  , Line 3: a₃x+b₃y+c₃=0 are concurrent if

Collinearity of Points

Three points A(x₁,y₁), B(x₂,y₂) and C(x₃,y₃)are collinear if

Angle between two Lines

Let the slope of two lines be m₁ and m₂. Then angle  between two lines is

                                              

Position of point w.r.t Line

Position of point A(x₁,y₁) and B(x₂,y₂) w.r.t line ax + by+c=0.

If ax₁+by₁+c₁=0 and  ax₂+by₂+c₂=0 are of same sign, then points A and B lie on the same side of the line and if they are of opposite sign, then they lie on the opposite side of line.
 

Locus

Locus is a path trace by a moving or a variable point under certain given condition. If we find the equation of traced path, then the equation is the required locus.Steps to follow:

• Assume point (h, k) whose locus is to find

• Use the given condition

• Remove the variable

• After removing the variable, equation will be left in h, k and some fixed number. Finally replace ‘h’ by ‘x’ and ‘k’ by ‘y’ to get the required locus. 

Conic Section

Recognition of Conics

General form: ax²+2hxy+by²+2gx+2fy+c = 0

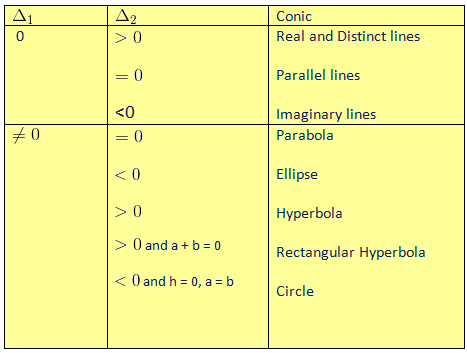
Eccentricity

Let P be any moving point and S be the focus (fixed point) of the conic. Let PM be the perpendicular distance of the point from the directrix (fixed line) of the conic. Then eccentricity or contracity ‘e’ of the conic is defined by

Note: ‘e’ can never be negative.

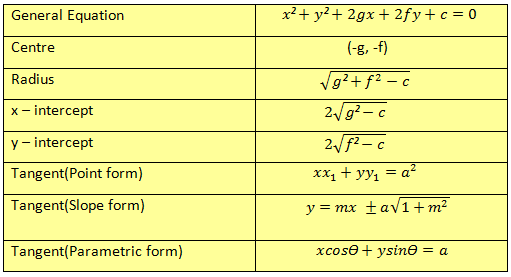
Circle

 

Parabola

Ellipse

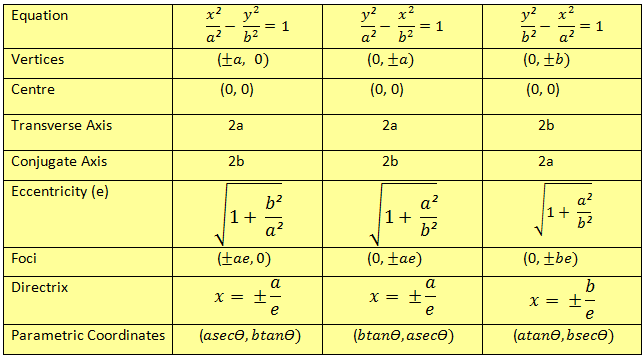
Hyperbola

Some Interseting Facts

• The locus of a point from which the distance of two tangents to a circle are equal is radical axis.

• Minimum distance between any two curves always lies along the normal.

• PQ be the focal chord of parabola and S be the focus of the parabola. Then, SP, 2a and SQ are in Harmonic progression.

• Tangents at the extremities of the focal chord intersect at right angle on the directrix.

• If a triangle is formed by joining the foot of normals which are concurrent on the parabola, then centroid of parabola will always lie on the axis of parabola.

• Locus of all those points which divide the perpendicular drawn from any point on the circle to any one of the fixed diameter in a constant ratio is an ellipse.

• Auxiliary circle ia a circle concentric with the ellipse and having diameter equal to the major axis of the ellipse.

• Maximum four normals can be drawn to ellipse.

• If the two circles of different radii touchs each other externally, then the locus of centre of the third of variable radius which touches these two circles externally is hyperbola.

• The locus of all points from where perpendicular tangents are drawn to the hyperbola is the director circle of the hyperbola.

Is coordinate geometry an important part of IIT – JEE preparation? 

Coordinate geometry is an important part of JEE maths paper. It can really improve your rank. Each year in the JEE mathematics, we have around 20% - 25% of the total marks of mathematics from this part. Among the coordinate geometry, almost 50% of the total question cover from the straight line and the circles.

Books to Refer

• Coordinate Geometry by SL Loney

• Arihant Coordinate Geometry

• Tata Mcgraw Hill for IIT – JEE

Tips to study Coordinate Geometry

In coordinate geometry students are less likely to commit mistake. However due to lack of the conceptual clarity and less input time to the topics, people often commit silly mistakes. This is an extremely scoring topic in JEE mathematics which can get you better rank in the JEE. Here are some tips which you must follow to score high in this branch:

• Do not practice a single problem in coordinate geometry without drawing a figure.

• Important results should be on your tips which might prove helpful in many of the objective problems.

• Make a different notebook for the formulas. Write all the important formulas in your notebook on daily basis.

• Try to memorize as much formulae as you can.

• Read the question clearly to figure out what it actually demands. It might save your time.

• Do not read the same concept from different books as it will lead to confusion. Always stick to one particular standard text for your concepts (Class notes or SL Loney).

• Practice as many problems as you can from the reference books. Then try to solve the previous year JEE paper problems of coordinate geometry.

• Try your level best to solve a problem before referring its solution.

Practical Application of Coordinate Geometry

Coordinate geometry is used extensively in daily life problems. Here are some of the examples

• Coordinate geometry is used in astronomy particularly in computing the paths of celestial bodies like planets, comets, binary star system etc.

• Coordinate geometry is used in the study of the paths of projectile like missile and other arms.

• Coordinate geometry is extremely useful in the aircraft industry, specifically when dealing with the shape of an airplane's fuselage. Conic curves are used to describe the fuselage cross sections and their curvature is modified along the length of the fuselage to render a smooth yet producible surface which at the same time should allow for an efficient internal arrangement.

• Computer programmers use coordinate geometry because most of the program they write generate PDF files. And in a PDF file the printed page is one big coordinate plane. Coordinate geometry is thus used to position elements on the page. PDF files that are produced contain text, images and line drawing, all of which are placed into position by using (x, y) coordinates, distances and slopes.

• Coordinate geometry is also used in manipulating images. The selected image is a big plane coordinate with each colour information as a single individual point. Thus when the colours of the pictures are being manipulated, the points are changed.

• Coordinate geometry is also used in the scanners. Scanner make use of the coordinate geometry to reproduce the exact image of the selected picture in the computer. It manipulates the points of each information in the original documents.

 

You Might Like to Refer:

CBSE online class 12 maths | CBSE online class 12 science | CBSE Class 9 Coaching