Parabola

 

Table of Content

Who came up with the Parabola? Meaning of Parabola Parabola in Conic Sections What is a Parabolic Curve? Terms related to Parabola What is the use of Parabola? Degenerate form of parabola Properties of Parabola Equation of Parabola General form of equation of Parabola Standard form of equation of Parabola Vertex form of equation of Parabola How do you find the focus of a Parabola? How to graph a Parabola?

Who came up with the Parabola?

Menaechmus was first to discover a method to solve the problem about the doubling of cube with using parabolas. Archimedes figured out the area surrounded by a parabola and a line segment Apollonius gives the name "parabola" .Pappus proved the properties of the focus and directrix of the parabola.
 

Meaning of Parabola

Parabola is basically a curve or path followed by a ball when it got kicked .when we kick a ball, it goes up and then come down while making a U shaped curve which is called Parabola.

As the word parabola itself describes the meaning that is, “para” means “for” and “bola” means “throwing”. Altogether it means the shape or curve made by kicking or throwing a ball in the air.

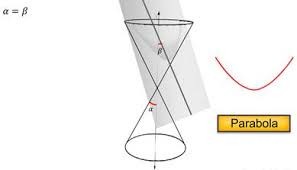
Parabola in Conic Sections

Parabola is formed in conic sections when a plane intersects the right circular cone in such a way that the angle between the vertical axis and the plane is equal to the vertex angle, that is, α = β. Parabola is an open curve at the intersecting surface of the cone.

What is a Parabolic Curve?

Parabolic Curve is defined with the help of a point and a line. Parabolic curve is a locus of all the points on the plane which have same distance from a line called Directrix and a fixed point called Focus. A parabola does not have a center.

Here, F is the fixed point called focus, l is the fixed line called Directrix. P₁, P₂ and P₃ are the different points on the plane. This shows that the distance from focus to point on plane and to directrix is equidistant for all the points on plane. Like:

FP₁= P₁B₁

FP₂ = P₂B₂

FP₃ = P₃B₃
 

Terms related to Parabola

• Directrix -  It is the line perpendicular to the axis of symmetry but not passes through the focus.

• Focus - It is a special point on the axis of symmetry which defines the parabola. Parabola is a special case of ellipse in which one of the foci is at the point of infinity.

• Axis of Symmetry - It is a line which divides the parabola in two equal parts that is, it is the line of symmetry of parabola .It is perpendicular to the directrix and passes through the focus.

• Vertex - The point where the parabola and the axis of symmetry intersects with each other is called vertex. At vertex the parabola is abruptly curved.

• Focal Length - It is the distance between the vertex and the focus on the axis of symmetry.

• Latus Rectum - It is a line segment parallel to the directrix and passes through the focus of the parabola.
   

What is the use of Parabola?

It is the reflective property of parabola which makes it useful in so many fields.

The rays of light or sound which are parallel to the axis of symmetry get reflected to the focus after touching the surface of the plane.

Uses of Parabola:

• Headlights of car

• Torches

• Radio Antenna

• Radar dishes

• Satellite dishes
   

Degenerate form of parabola

If the focus lies on the directrix, so that the same distance of directrix and focus together form a straight line then it is the degenerate case of parabola. The vertex lies on the axis of symmetry and perpendicular to the directrix.

Or in conics if a plane intersects the double right circular cone at the vertex of the cone, such that α = β and the plane contains a generator of the cone and the section is a straight line is called degenerate conics in case of parabola.
 

Properties of Parabola

• Focus of Parabola: Focus is a point from which the distance is measured to form conic. The parabola has the vertex as the midpoint of the focus and the directrix.

• Eccentricity of Parabola: Eccentricity is the factor related to conic sections which shows how circular the conic section is. More eccentricity means less spherical and less eccentricity means more spherical. It is denoted by“e”. The eccentricity of parabola is the ratio of the distance between the focus and a point on the plane to the vertex and that point only. As the parabola is a locus of all the points which are equidistant from the focus and the directrix, its ration will always be 1 that is, e = 1

• Latus rectum of Parabola: It is the line parallel to directrix and passes through the focus of parabola. It is perpendicular to the axis of symmetry. In parabola, let a is the distance from focus to the vertex, which is equidistant from the vertex to directrix.so the distance from focus to directrix is 2a. The distance from the focus to the point on plane is equidistant from focus to directrix that is, 2a. Focus is on the axis of symmetry which is the midpoint of latus rectum, which shows that the half of latus rectum is 2a and the length of latus rectum is 4a.

Equation of Parabola

General form of equation of Parabola

Ax² + Bxy + Cy² + Dx + Ey + F = 0

The expression B² - 4AC is the discriminant which is used to determine the type of conic section represented by equation.

If equation fulfills these conditions, then it is parabola.

B² -  4AC = 0

Example

Given equation is 6x² + 12x – y + 15 = 0, find whether it is the equation of parabola or not?

Solution: Here A = 6, B = 0, C = 0

Determinant will be B² - 4AC

= 0-4(6) (0) = 0

This shows that B² - 4AC = 0 so this is parabola or in other way we can say that only one variables is squared, so this is parabola.

Standard form of equation of Parabola

Cartesian coordinates are the points on a plane with a pair of numerical coordinates which represented by (x, y)

 If the vertex is at the origin and the axis of symmetry lies on x-axis

There will be two situations possible if the vertex is at the origin and the axis of symmetry lies on the x-axis, the parabola is either on the positive side of x- axis or on the negative side of the x-axis.

• If p >0 and  pw lies on the positive x-axis

y² = 4px

Here, p is the distance from vertex to focus on the x axis. So the coordinates of F = (p, 0), which shows that it lies on the positive side of x-axis. Directrix is at x = -p, as it is equidistant from the vertex as vertex is from focus. This shows that if p > 0, then the parabola opens towards right.

• If p < 0 and p lies on negative x-axis

y² = -4px

Here, p is the distance from vertex to focus on the x axis, which is negative. So the coordinates of F = (-p, 0), which shows that it lies on the x-axis, but on the negative side.

Directrix is at x = p, as it is equidistant from the vertex as vertex is from focus .this shows that if p < 0, then the parabola opens towards left.

 If the vertex is at the origin and the axis of symmetry lies on y-axis

There will be two situations possible if the vertex is at the origin and the axis of symmetry lies on the y-axis that the parabola is either on the positive side of y- axis or on the negative side of the y-axis.

• If p >0 and p lies on the positive y-axis

x² = 4py

Here, p is the distance from vertex to focus on the y-axis. So the coordinates of F = (0, p), which shows that it lies on the y-axis.

Directrix is at y = -p, as it is equidistant from the vertex as vertex is from focus .this shows that if p > 0, then the parabola opens upwards.

• If p < 0 and p lies on negative y-axis

​x² = -4py

Here, p is the distance from vertex to focus on the y axis, which is negative. So the coordinates of F = (0,-p)), which shows that it lies on the y-axis, but on the negative side.

Directrix is at x = p, as it is equidistant from the vertex as vertex is from focus .this shows that if p < 0, then the parabola opens downwards.

Vertex form of equation of Parabola

If the vertex is not at the origin

• x = p(y - k)²+ h

where p is the horizontal stretch factor, (h, k) is the coordinates of the vertex. This shows that if p > 0 that is, p is positive then the parabola opens towards right and if p < 0 that is, p is negative then the parabola opens towards left.

• y = p(x - h)2 + k

where p is the vertical stretch factor. (h, k) is the coordinates of the vertex. This shows that if p > 0 that is, p is positive then the parabola goes upwards and if p < 0 that is, p is negative then the parabola goes downwards.

How do you find the focus of a Parabola?

If we have an equation of a parabola in vertex form like y = a (x−h)² + k, it means that the vertex is at (h, k) and the focus is (h, k+1/4a)

As we know that this equation is for vertical parabola, so the x-coordinate of the focus will be same as the x-coordinate of the vertex.

Example

Find the focus of the parabola y = -2(x + 4)²-1.                       

Solution: As this equation is given in vertex form we can easily identify the coordinates of the vertex that is, (-4,-1) and a = -2.

This shows that a <0 so the parabola will go downward on the y axis.

Now we will find

 1/4a

As a = -1 so it will be -1/8

So the coordinates of focus will be (h, k + 1/4a)  = (-4,-1 + -1/8)

= (-4, -9/8)
 

How to graph a Parabola?

To draw a graph of parabola we must know the vertex of the parabola and the focus. We will use the vertex and standard form of equation to draw the graph as it shows the coordinates of vertex and the position of the parabola.

• If the vertex is at origin: It is easy to draw parabola if its vertex is at the origin.

Example 

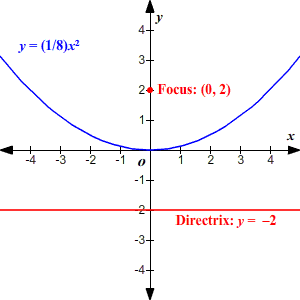Draw the graph of the parabola with equation y= (1/8)x²

Solution: Here we know that the (h, k) = (0, 0), so the vertex is at the origin.

Now we have to find the focus that is, (h, k+1/4a)

Given a = 1/8

On solving the equation we will get it 2

So the coordinates of focus is (0, 2)

Now we will count till 2 on y axis up for the focus and down for the directrix

• If the vertex is away from the origin: If we have to draw a parabola which has its center away from the origin that is, the vertex  point must be something (h,k).Then we will plot the vertex at (h,k) then count till a on the major axis and till b on the minor axis and will draw parabola accordingly.

Example

Draw a graph of parabola with equation

y = (x – 2)² - 3

Solution: Here we know the vertex of the parabola by the equation, (h, k) = (2, -3), a = 1. This equation shows that it is a vertical parabola and going upwards as a >0.

So first we will first plot the vertex of the parabola on the graph with the coordinates (2, - 3). Then we will calculate F which is (h, k+1/4a)

The coordinates of F = (2,-2 ¾)

Now we will plot the points for the focus.

After plotting all the points we will make a curve joining all the points which will turn out to be a vertical parabola.
 

Watch this Video for more reference
 

More Readings