Hyperbola

Table of Content

History of Hyperbola
Meaning of Hyperbola
Hyperbola in Conic Sections
Terms related to Hyperbola
Degenerate form of Hyperbola
Properties of Hyperbola
Equation of Hyperbola
- General form of equation of Hyperbola
- Standard form of equation of Hyperbola
Graph of Hyperbola
Hyperbola vs.Parabola

History of Hyperbola

Menaechmus discovered Hyperbola in his investigations of the problem of doubling the cube. The name of hyperbola is created by Apollonius of Perga.Pappus considered the focus and directrix of hyperbola.

Meaning of Hyperbola

Hyperbola is a mirror image curve of parabola. It is a locus of all the points on the plane which have the constant ratio of difference between the distances from two fixed points called foci. Here the difference means the farthest distance minus shortest distance.

Hyperbola in Conic Sections

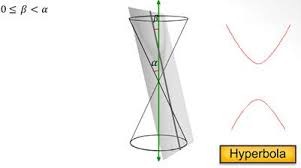
Hyperbola is formed in conic sections when a plane intersects the right circular cone in such a way that the angle between the plane and the vertical axis is less than the vertical angle that is, 0 ≤ β < α. In all the other conic sections the plane cuts only one nappe of the cone but in case of hyperbola the plane cuts the two nappes of the cone so that two disjoint open curves are formed called Hyperbola.

Terms related to Hyperbola

Focus - The two fixed points which defines the hyperbola are called the focus together called Foci.
Center - It is the midpoint of the line segment which joins the two foci. Or the intersection point of the transverse axis and the conjugate axis.
Transverse Axis - It is a line passes through the two foci. It is also called the major axis of hyperbola.
Conjugate Axis – It is the line perpendicular to transverse axis and passé through the center of the hyperbola.
Vertex - The two points where the hyperbola intersects with the transverse axis are called the Vertex together called Vertices.

Degenerate form of Hyperbola

When a plane intersects the right circular cone in such a way that it passes through the apex and parallel to the axis of symmetry then it results in the two intersecting lines. O r When 0 ≤ β < α, the section is a pair of two intersecting straight lines.

Properties of Hyperbola

(1) Focus of Hyperbola (2) Asymptotes of Hyperbola (3) Eccentricity of Hyperbola (4) Latus rectum of Hyperbola (5) Semi Latus Rectum (6) Rectangle in Hyperbola

1. Focus of Hyperbola

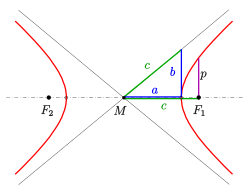
Focus is a point from which the distance is measured to form conic. The Hyperbola has two foci.to calculate the focus we can use the formula

c is the distance between center and one of the foci. If the coordinate of center is (h, k) then the coordinates of the foci will be (h−c, k) and (h+c, k) in horizontal hyperbola and (h, k−c) and (h, k+c) in vertical hyperbola.

2. Asymptotes of Hyperbola

These are the two intersecting straight lines in a hyperbola which intersects at the center. If a hyperbola retreats from the center, its branches approach these asymptotes. The equation of asymptotes are:

y = (b/a) x

y = − (b/a) x

3. Eccentricity of Hyperbola

Eccentricity is the factor related to conic sections which shows how circular the conic section is. More eccentricity means less spherical and less eccentricity means more spherical. It is denoted by“e”.

The eccentricity of Hyperbola is the ratio of the distance between the focus and a point on the plane to the vertex and that point only.

As the Hyperbola is a locus of all the points which are equidistant from the focus and the directrix, its ration will always be 1 that is, e = c/a

where,

In hyperbola e>1 that is, eccentricity is always greater than 1.

4. Latus rectum of Hyperbola

It is the line perpendicular to transverse axis and passes through any of the foci of the hyperbola. It is parallel to the conjugate axis.

In Hyperbola, latus rectum is 2b²/a.

5. Semi Latus Rectum

It is the half of the latus rectum as shown in the above picture as p. so p = b²/a.

6. Rectangle in Hyperbola

It is the rectangle made by the and b which helps in drawing the hyperbola. a is the distance between the center and the vertex, b is the half length of the conjugate axis and c is the distance between center and the focus. The diagonal of this rectangle intersects at the center and these diagonals are the asymptotes of hyperbola.

Equation of Hyperbola

(1) General form of equation of Hyperbola (2) Standard form of equation of Hyperbola

1. General form of equation of Hyperbola

Ax² + Bxy + Cy²+ Dx + Ey + F = 0

The expression B² - 4AC is the discriminant which is used to determine the type of conic section represented by equation.

If equation fulfills these conditions, then it is Hyperbola.

B² - 4AC > 0

Example

Given equation is x² – y² + 3x – 2y – 43 = 0, find whether it is the equation of Hyperbola or not?

Solution

Here A = 1, B = 0, C = -1

Determinant will be B²-4AC

= 0-4(1) (-1) = 4

This shows that B² - 4AC > 0 so this is Hyperbola or in other way we can say that both variables are squared, and the squared terms have opposite signs, so this is a hyperbola.

2. Standard form of equation of Hyperbola

Cartesian coordinates are the points on a plane with a pair of numerical coordinates which represented by (x, y)

If the center is at the origin: There are two possibilities of hyperbola if the center is at the origin that either it is vertical hyperbola or horizontal hyperbola.

the foci is on x-axis

where a is the distance between center and the vertex. So the coordinates of two vertices are:

(a, 0) and (-a, 0)

the foci is on y-axis

where a is the distance between center and the vertex. So the coordinates of two vertices are:

(a, 0) and (-a, 0)

if the center is not at the origin: There are two possibilities of hyperbola if the center is not at the origin that either it is vertical hyperbola or horizontal hyperbola.

The foci is on x-axis

The foci is on y-axis

Graph of Hyperbola

To draw a graph of Hyperbola we must know the center of the Hyperbola. We will use the standard form of equation to draw the graph as it shows the coordinates of center and b of the Hyperbola.

If the vertex is at origin: It is easy to draw Hyperbola if its center is at the origin.

Example

Draw the graph of the Hyperbola with equation

Solution:

Here we know that the (h, k) = (0, 0), so the center is at the origin.

Given a = 2 and b = 3

We have to first mark the center at the origin.

Then count till 2 on transverse axis both left and the right.

Then count till 3 on conjugate axis both up and down.

We don’t have to join these dots, otherwise it will make an ellipse. So we have to make a rectangle with these dots, and then make the diagonals of this rectangle which will be the asymptotes of the hyperbola.

Now draw the curve.

If the vertex is away from the origin If we have to draw a Hyperbola which has its center away from the origin that is, the center point must be something (h, k).Then we will plot the center at (h, k).

Example

Draw a graph of Hyperbola with equation

Solution:

Here we know the center of the Hyperbola by the equation, (h, k) = (-3, 3), a = 4 and b = 3 .This equation shows that it is a vertical Hyperbola.

So first we will plot the center of the Hyperbola on the graph with the coordinates (-3, 3).

The vertices are 2a so it is 8.

The center is midpoint of the two foci.to calculate the foci we will use the formula b²= c²- a²

a = 3 and b = 4 so c²= 16 + 9 = 25

c = 5

So we will count till 5 up and down from the center to mark the point of the two foci which is (-3, 8) and (-3,-2)

The coordinates of the vertex are (-3, 0) and (-3,-6)

Now using all the points we can draw the graph of vertical hyperbola easily.

Hyperbola vs. Parabola

		Parabola	Hyperbola
1	Definition	Parabola is formed in conic sections when a plane intersects the right circular cone in such a way that the angle between the vertical axis and the plane is equal to the vertex angle, that is, α = β.	Hyperbola is formed in conic sections when a plane intersects the right circular cone in such a way that the angle between the plane and the vertical axis is less than the vertical angle that is, 0 ≤ β < α.
2	Meaning	It is a locus of all the points on the plane which have same distance from a line called Directrix and a fixed point called Focus.	It is the set of all points where the difference in the distance from two fixed points together called Foci is constant.
3	Intersection of plane	Plane intersects with only one nappe of the cone.	Plane intersects with both the nappe of right circular cone.
4	Degenerate form	a line.	two intersecting straight lines.
5	Eccentricity	e = 1	e > 1
6	Latus rectum	4a	2b²/a
7	Focus	(h, k+1/4a)	so that the two foci are (h−c, k) and (h + c, k)
8	Center	Does not have a center	The midpoint of two foci is called Center
9	Equation with center or vertex at origin	y² = ± 4px(horizontal) x² = ± 4py(vertical)
10	Equation with center or vertex not at origin	x = ± p(y - k)² + h (horizontal) y = ± p(x - h)² + k(vertical)

More Readings

Hyperbola

Related Resources:

Refer the Useful Books of Mathematics here.
Refer the Revision Notes on Hyperbola for a quick revision.

To read more, Buy study materials of Hyperbola comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.