Ohm’s Law

 

Table of contents

Voltage, Current and Resistance Ohm’s Law Derive Ohm’s Law Applications of Ohm’s Law Power and Ohm’s Law Summary

Voltage, Current and Resistance

The terms used in ohm’s law are voltage, current and resistance. Voltage can be defined as the pressure which tries to push the electrons through the wires in a circuit. It is the driving force to produce electricity. Voltage is measured in volts. Current can be defined as the rate of flow of electrons in a circuit. The unit of current is amperes. Resistance will resist the flow of electrons in a circuit and thus it can affect the current that flows in circuit.

Consider a circuit in which a battery or a cell and a resistor is connected. The battery or the cell creates a potential difference and as a result the charges particles known as the electrons flows along the circuit. The resistors connected in the circuit makes an attempt to prevent the flow of electrons. Current is the number of charged particles that passes in each second. When we use more cells in a circuit, the voltage along the circuit increases. Thus the current increases when the voltage increases.

The current flowing in the circuit can also be increased by using a resistor of small resistance. When we connect resistors in parallel, the flow of current increases. Resistors connected in parallel is as same as a single resistor with a low resistance connected in a circuit. When resistors are connected in series, it is the same as a single resistor with high resistance connected along the circuit.
 

Ohm’s Law

It was George Simon Ohm who formulated the Ohm’s law. He stated that the electric current that flows through a wire will be directly proportional to the potential difference across the ends when the temperature remains constant. That constant is nothing but the resistance. The resistance of a material is constant when the temperature remains constant. V = I R. Ohm’s law is considered as one of the most basic law in the field of electronics. Thus

Voltage V = Current * Resistance = I R

Current I = Voltage / Resistance = V / R

Resistance R = Voltage / Current = V / I

Ohm’s law

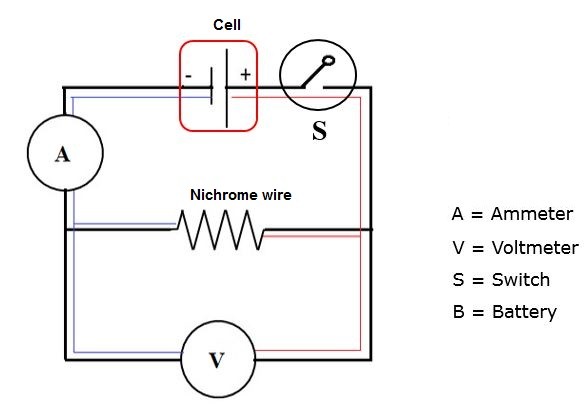
Consider a circuit which consists of a cell of 1.5 V, an ammeter, Voltmeter, a switch and a nichrome wire. Connect the cell and the switch is in on position now. Now the ammeter shows the reading as 0.12 A and e voltage is 0.3 V. When two cells are connected the current shown in the ammeter changes to 0.2 A and voltage is 0.5 V. Again when three cells are connected in the circuit it shows 0.3 reading in ammeter and 0.75 V in the voltmeter. Thus we can see that when the number of cells increases, the value of current and voltage also increases. So it is clear that voltage is directly proportional to current.

Circuit to prove ohm’s law

Number of cells	Voltage	Current
1	0.3 V	0. 12 A
2	0.5 V	0. 2 A
3	0.75 V	0.3 A

We can also see that the ratio of voltage to current that is V / I is a constant for all the readings. The constant is considered as R. So V= I R. The voltage current graph will be a straight line.

The graph showing Ohm’s law

Here X axis represents the current and Y axis represents the voltage.
 

Derive Ohm’s Law

We know that ohm’s voltage is equal to current times resistance, that is V = I R. It says that the voltage is directly proportional to the current when the resistance is constant. The resistance of a material does not change when the temperature remains constant.

We know that the drift velocity, V_d  = - e E ԏ / m. Let this be equation 1, here e is the charge on an electron, E is the electric field, ԏ is the average time taken between each collision or the relaxation time of electrons and m is the mass of the electron. When an external electric field is applied across the conductor, the electrons drift to the positive or the higher potential end of the conductor at a certain velocity. This net velocity is called the Drift Velocity.

Also E = - V / L where V is the potential difference and L is the length. Electric field is the negative gradient of electric potential. 

Also E = - V / L where V is the potential difference and L is the length. Electric field is the negative gradient of electric potential.

Substituting the value of E in the first equation we get V_d  = e V ԏ / m L. 

From this equation, we get V = V_d m L / e ԏ - equation 2. 

Current I = A n e V_d, where A is the area of the cross section of the wire, n is the charge density, e is the charge on current carriers or electrons, V_d is the drift velocity.

From the equation, we get V_d = I / A n e.

Substituting this value of V_d  in equation 2 we get V = I / A n e *( m L / e ԏ)

Re arranging the equation, we get V = (m L / A n e² ԏ) I – equation 3

We can say that (m / n e² ԏ) * L /A = R, the resistance and also we know that R = ρ * L / A

 So, m / n e² ԏ = ρ 

Thus, substituting the values in the equation 3 we get, V = ρ * L / A * I

= R I

Thus V = I R. Finally, we derived the ohm’s law and it is proved.
 

Applications of Ohm’s law

Based on ohm’s law there are a lot of applications seen in our day to day life. Ohm’s law is applicable to both direct current circuits and alternating current circuits. The law is applicable for linear circuits. A linear circuit is also known as Ohmic Circuit where voltage to current ratio maintains a constant ratio. Ohm’s law cannot be applied to diodes, electrolytes etc. as they come under the category of non – linear circuits. The resistance that can be increased or decreased in a potentiometer is based on ohm’s law. Other laws related to electric current like Kirchhoff’s law is arrived from ohm’s law.

The transformers and generators follows the ohm’s law. Electric heaters and incandescent bulbs and many other electrical appliances work under the principle of ohm’s law. We can also determine the power developed or the power lost in the electronic devices. It is possible to find the values of voltage, current and resistance through ohm’s law. We can also find the equivalent resistance of both series and parallel circuits using ohm’s law.

The law is not applicable for unilateral networks and non – linear elements. When the resistance changes due to the change in temperature, the ratio of voltage to current would not be the same numbers always. Thyristor, electric arc, diodes and LED s do not support Ohm’s law. The incandescent bulb does not follow Ohm’s law as the resistance of the wire changes when it is heated up due to increase in current and voltage. Semi – conductors like Germanium and silicon do not support Ohm’s law. Non – ohmic conductors are the ones which does not obey ohm’s law. Non – ohmic circuits consists of non – ohmic elements.

Power and Ohm’s Law

We know that power is rate of doing a work. It is the rate at which the energy is either taken in or given out in a circuit. The unit of power is watt.

Power P = Voltage * Current = V * I

From ohm’s law we get I = V / R. Substituting this value we get P = V * V /R = V² / R.

Also V = I R. Substituting we get I R* R = I² R.

Ohm’s Law table

Voltage V =	I*R	√(PR)	P/I
Current I =	V/R	√(P/R)	P/V
Resistance R =	V/I	P/I2	V2/P
Power P =	V*I	I2R	V2/R

Ohm’s law Pie chart

Problems

A circuit has a battery voltage of 20 V. A lamp resistance of 5 Ω is connected to the circuit. Calculate the current and the power of the circuit.

Solution:

Current I = Voltage / Resistance = 20 / 5 = 4 A.

Power P = Voltage * Current = 20 * 4 = 80 watts. The lamp gives out 80 W of power in the form of heat and light.

Or Power P = I ² R = 4 ² * 5 =16 * 5 = 80 watts

Or Power P = V ² / R = 20 ² / 5 = 400 / 5 = 80 watts.
 

Summary

• George Simon Ohm formulated the Ohm’s law.

• The electric current that flows through a wire will be directly proportional to the potential difference across the ends when the temperature remains constant. Thus Voltage V = Current * Resistance (I R), Current I = Voltage / Resistance = V / R.  Resistance R = Voltage / Current = V / I.

• Voltage can be defined as the driving force to produce electricity. Current is the rate of flow of electrons in a circuit. The resistance restricts the flow of electrons in a circuit.

• The laws related to electric current like Kirchhoff’s law is arrived from ohm’s law. The law is applicable for linear circuits. It is otherwise known as ohmic circuits.

• We can find the values of voltage, current and resistance by ohm’s law.

• Transformers, generators, electric heaters and incandescent bulbs, all are designed under the principle of ohm’s law.

• The law is not applicable for unilateral networks and non – linear elements.

• Power, P = V * I, P = V² / R, P= I² R.

Watch this Video for more reference
 

 

More Readings

Ohm’s Law