Meter Bridge
Table of contents |
Wheatstone Bridge
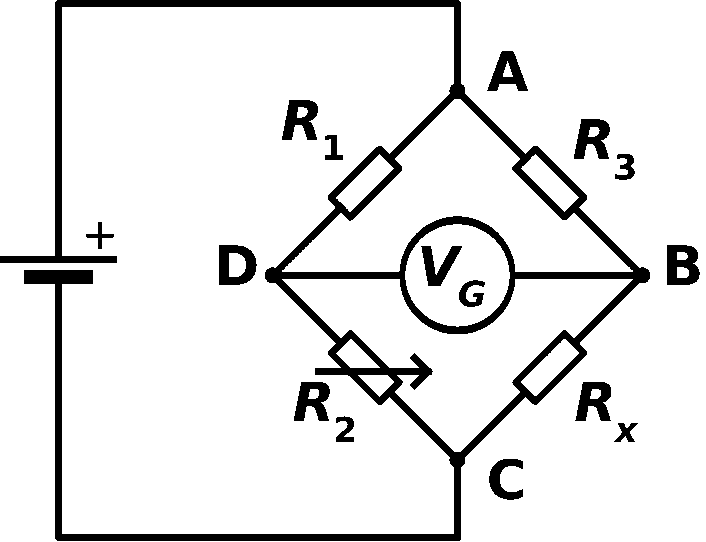
Meter Bridge is an instrument that is used to find the unknown resistance of a coil or any other material. This bridge works under the principle of Wheatstone bridge. We know that the Wheatstone Bridge is used to measure the unknown resistance connected in a circuit. It consists of four resistors of which two resistors are known Resistors, one variable resistor and one unknown resistor. It also consists of a galvanometer. The bridge has two series-parallel arrangements of resistors. The figure of Wheatstone bridge is shown below:
Wheatstone bridge
It consists of four arms AD, DC, CB and BA which has fixed and variable resistors. Resistors resists the flow of electric current. Its measure is called resistance. Here R1 and R3 are the fixed resistors and R2 is the variable resistor and Rx is the unknown resistor. The variable resistor is the resistor which restricts and also can control the flow of electric current. It can control the flow of current by either increasing or decreasing the value of resistance. Here AD and BA are the ratio arms. A galvanometer is connected between the terminals D and B. So they are called as the Galvanometer Arm. As the cell is connected between the terminals A and C, it is called battery arm.
Here by adjusting the value of the variable resistor R2 we will make the deflection in galvanometer as zero. The bridge is said to be balanced when no current flows through the galvanometer. When there is no current flowing through the bridge the potential difference or voltage between the points D and B is zero. Here the current flowing through the fixed resistor R1 and the variable resistor R2 is the same and is considered as I1. The current flowing through the fixed resistor R3 and the unknown resistor Rx will be the same and is I2. When the potential at D and B is the same, the voltage drop from the point A to D is equal to the voltage drop at from point A to point B.
By applying Kirchhoff’s law we get I1 R1 - I2 R3 = 0. That is I1 R1 = I2 R3. Kirchhoff’s voltage law states that the algebraic sum of all voltages within the loop will be equal to zero.
Now the voltage drop from point C to point D is equal to the voltage drop from point C to B. So I1 R2 - I2 RX = 0. Thus I1 R2 = I2 RX.
Now divide the equations
Thus Rx = R2 R3 / R1. Finally the unknown resistance is determined in terms of other known Resistors of the Bridge.
The applications of the Wheatstone bridge include strain gauge, thermistor, potentiometer, light detector etc. Wheatstone bridge are also used in operational amplifier as it can measure and amplify the small changes that takes place in resistors.
Meter Bridge
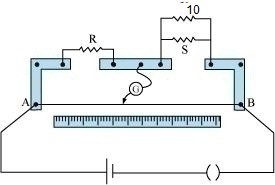
Meter bridge is also known as the Slide Wire Bridge. It consists of a wire whose length is one meter and has uniform cross sectional area. Now the wire is stretched along a meter scale. The bridge has two metallic strips which is in reverted L shape on either side of the wire. These metallic strips act as holders for the wire. The wire is being clamped to the strips.These two metallic strips are made up of metals like copper. The bridge consists of another metallic strip which is placed between those two strips with a gap between them. So totally there are five leads on the bridge.
Meter bridge
A resistance box R and an unknown resistance S is connected across the two gaps of the metallic strips as shown in the figure. One end of the galvanometer is connected to the middle lead of the metallic strip which is placed between the L shaped strips. The other end of the galvanometer is connected to a jockey. The jockey is used to slide on the bridge wire. It is a metal rod with one end as knife edge.
Meter Bridge
Now adjust the value of resistance in the resistance box and slide the jockey along the wire. This process is to be done until the galvanometer shows a zero or null deflection. Consider at point B the galvanometer showed zero deflection. So now the jockey is connected to the point B on the wire. Thus the distance from the point A to B is taken as L1 cm. Then the distance from point B to point C is L2 cm that is 100 - L1 cm. Now the meter bridge becomes similar to the Wheatstone bridge. The meter bridge now is drawn as Wheatstone bridge for more clearance.
Meter bridge to Wheatstone bridge
We know that R = ρ L /A, where R is the resistance, ρ is the resistivity, L is the length of the wire and A is the area of cross section of the wire. So the resistance across the portion AB of the wire is Rw L1 and that the resistance across the point BC is Rw (100 - L1). Rw is the resistance of the whole wire. That is according to Wheatstone bridge we get

This is the equation
So to find the unknown resistance S we have S = R (100 - L1) / L1
Lab Experiment
If we are doing the meter bridge experiment in the lab, by adjusting the value of resistance box the galvanometer will show the null deflection. Then we will find the value of L1 and L2. After substituting these values in the equation we will find the unknown resistance. Now the process is being repeated for a number of values of resistance by adjusting the values resistance box. Then finally we will get the actual unknown resistance by calculating the mean of the unknown resistance. That is, total sum of unknown resistance / no of times the readings have been taken.
Also the specific resistivity of the material of the wire is ρ = π r2 X/L, where r is the radius of the wire, X is the unknown resistance and L is the length of the wire.
Problem Related with Meter Bridge
Q1. In a meter bridge, there are two unknown resistance R1 and R2. Find the ratio of R1 and R2 if the galvanometer shows a null deflection at 30 cm from one end?
Solution:
The null deflection in the galvanometer is given as 30 cm from one end.
So consider L1 = 30 cm
So L2 = 100 – 30 = 70 cm
Thus the ratio of the unknown resistance can be found as

Thus R1: R2 = 3: 7
Q2. In the meter bridge, the null deflection is shown on the galvanometer which is at a distance of 30 cm from one point. When a known resistance of 10 Ω is connected in parallel with another unknown resistance S the null deflection shows at 50 cm from the same point. Find the unknown resistance of R and S.
Meter bridge
Solution:
In the first case L1 = 30 cm

As the resistors are connected in parallel we know that the equivalent resistance is R1 R2 / R1 + R2
= 10 * S / 10 + S
In the second case L1 = 50 cm So L2 = 100 – 50 = 50
So according to the formula
R / S = 1
= R / (10 S / 10 + S) = 1
So R = 10 S / 10 + S
Substituting the value of R in equation 1we get

From equation 1 we get

Q3. A 20 Ω resistor is connected in the left gap and an unknown resistance is connected in the right gap of the meter bridge. Also the null deflection point is shifted by 40 cm when the resistors are interchanged. Find the value of unknown resistance?
Solution:
In the first case the deflection point is taken as L1. Let the balance point gets shifted to L2 by 40 cm when the resistors are interchanged.
So we get L1 - L2 = 40
Also we know L1 + L2 = 100
Solving these two equations we get L2 = 30 cm and L1 = 70 cm.

Conclusion
-
The meter bridge uses the same principle as the Wheatstone Bridge.
-
It is used to find the unknown Resistance of the Material.
-
The meter bridge consists of a wire of 100 cm, a scale, one unknown Resistor, one known Resistor or a Resistance Box, a Galvanometer and a jockey.
-
For finding the unknown Resistance, connect everything as required. Now until the galvanometer shows a zero or null deflection, adjust the value of resistance in the resistance box and slide the jockey through the wire. Measure the length of the wire L1 at which the galvanometer showed null deflection. Calculate the length L2. Then by using the Wheatstone bridge principle we can find the unknown Resistance of the Meter Bridge. The Meter Bridge is also known as Slide Wire Bridge.
Watch this Video for more reference
More Readings