a)) show that the distance d between the parallel lines Ax+By+C1=0 and Ax+By+C2=0 in the plane is :
d=l C1 - C2 l/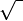 A^2 + B^2
A^2 + B^2
b)) use this result to find the distance between the parallel lines 2x+3y+17=0 and 4x+6y+31=0


Last Activity: 3 Years ago

Last Activity: 3 Years ago


Last Activity: 4 Years ago