Conjugate of a Complex Numbers

Conjugate of a complex number z = a + ib is denoted and defined by  = a-ib.

In a complex number if we replace i by -i, we get conjugate of the complex number.  is the mirror image of z about real axis on Argand's Plane.

Geometrical representation of conjugate of complex number -

           |z| = ||

        arg () = - arg (z)

        General value of arg ()= 2nΠ P.V. arg(z)

                

Properties:

(i) If z = x+y, then x= z+/2, y = z+/2

(ii) z =  = z is purely real

(iii) z +     = 0 = j is purely imaginary

(iv) ||2 = z 

(v)   = z

 

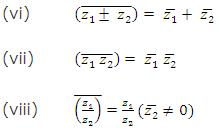
(ix) Imaginary roots of polynomial equations with real coefficient occur is conjugate pairs.

(x) If w=f(z), then    = f()

To read more, Buy study materials of Complex Numbers comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.