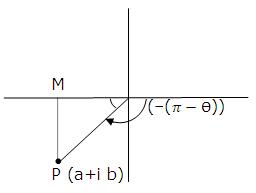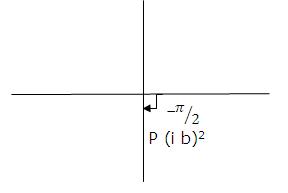Argument of a Complex Number

 

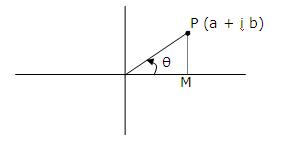
Argument of a non-zero complex number p(z) is denoted and defined by arg (z)= angle which OP makes with the positive direction of real axis.

If OP=|z| and arg (z)= θ, then obviously z=r (cos θ + i sin θ), called the polar form of z. 'Argument of z' would mean principal argument of z (i.e., argument lying in (-∏,∏ )) unless the context requires otherwise. Thus argument of a complex number z=a+ib = r (cos θ + i sin θ) is the value of θ satisfying r cos θ = a and r sin θ = b.

Let θ = tan^-1 |b/a|

(i)     a>0, b>0

P.V. arg z= θ

  

(ii)    a>0, b>0

P.V. arg z = ∏/2

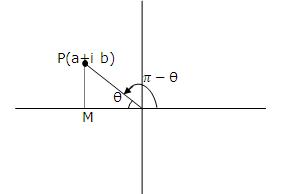
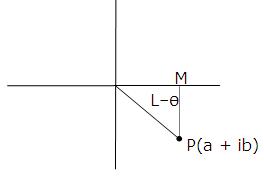
(iii)    a<0, b>0

 P.V. arg ∏ - θ

Argument of a non-zero complex number p(z) is denoted and defined by arg (z)= angle which OP makes with the positive direction of real axis.

If OP=|z| and arg (z)= θ, then obviously z=r (cos θ + i sin θ), called the polar form of z. 'Argument of z' would mean principal argument of z (i.e., argument lying in (-∏,∏ )) unless the context requires otherwise. Thus argument of a complex number z=a+ib = r (cos θ + i sin θ) is the value of θ satisfying r cos θ = a and r sin θ = b.

Let θ = tan^-1 |b/a|

(i)     a>0, b>0

P.V. arg z= θ

(ii)    a>0, b>0

P.V. arg z = ∏/2

(iii)    a<0, b>0

 P.V. arg ∏ - θ

(vii) a>0, b<0 

P.V. arg z=-θ

(viii) a>0, b=0

P.V. arg z = 0

To read more, Buy study materials of Complex Numbers comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.