0

Guest

Courses New

What is ans. Of ques. 5a and 6 plese see in the attatchment snd repy me

What is ans. Of ques. 5a    and 6 plese see in the attatchment snd repy me

Question Image
Grade:12

3 Answers

Soumendu Majumdar
159 Points
5 years ago
Dear Dushyant,
The image you’ve provided is not clear, please attach a closer & a clearer image in order for me to decipher the questions!
I’ll be happy to help you!
regards,
Soumendu
prince sunjot dutt
58 Points
5 years ago
5a) rate= -d[R]/dt=k[R]¹   ___ __  __ __ for first order reaction.
Wher, [R]= concentration of reactants.
d[R]/dt=-k[R]
d[R]/[R]= -kdt
∫ both sides
∫d[R]/R=∫-kdt 
ln[R]= –Kt+C. ______________1
When, t=0, R=[Ro]{initial concentration}
ln[Ro]= C
Therefore, 1=
ln[R]=-Kt+ ln[Ro]
kt=ln[Ro]-ln[R]
k=ln[Ro/R]/t
k=2.303log[Ro/R]/t viz the required equation.
 
 
 
Soumendu Majumdar
159 Points
5 years ago
Dear Dushyant,
Question-5:a) 

Let us use the following chemical equation: A ---> products.

The decrease in the concentration of A over time can be written as: - d[A] / dt = k [A]

Rearrangement yields the following: d[A] / [A] = - k dt

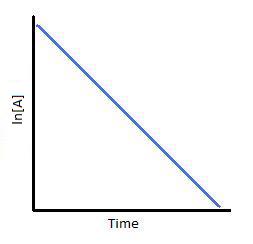
Integrate the equation, which yields: ln [A] = - kt + C

Evaluate the value of C (the constant of integration) by using boundry conditions. Specifically, when t = 0, [A] = [A]o. [A]o is the original starting concentration of A.

Substituting into the equation, we obtain: ln [A]o = - k (0) + C.

Therefore, C = ln [A]o

We now can write the integrated form for first-order kinetics, as follows:

ln [A] = - kt + ln [A]o

This last equation can be rearranged into several formats, such as:

ln ([A] / [A]o) = - kt

[A] / [A]o = 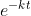e^{-kt}

[A] = [A]o 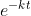e^{-kt}

Image05.jpg

Question-6:a) If [A]0 be initial concentration and k be rate constant then using above formula

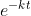
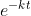[A] = [A]o e^{-kt}

e^{-kt} = 0.8  {For 20% completion, concentration of reactants is [A]0 – (0.2)[A]0}

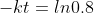
-kt=ln0.8

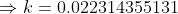\Rightarrow k = 0.022314355131 (You can round off the value as per your convenience)

Hence for 75% completion

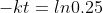
-kt=ln0.25

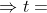
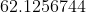
\Rightarrow t=62.1256744

So time taken for 75% completion is 62.126 minutes(approx).

Question-6:b) t1/2 is called half-life of the radioactive substance which is the time taken for its concentration to become half of its initial concentration.

Using above formula you will get

t1/2 = 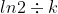ln2\div k

Also for 99.9% completion time taken is

t = 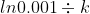ln0.001\div k

Hence their ratio is given by (or relation between them is)

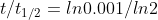
t/t_{1/2}= ln0.001/ln2

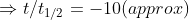
\Rightarrow t/t_{1/2}= -10(approx)

Hope it helps!

regards,

Soumendu

Think You Can Provide A Better Answer ?

Other Related Questions on Physical Chemistry

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More