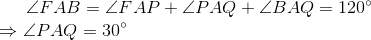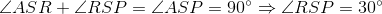Sandeep Pathak
Last Activity: 11 Years ago
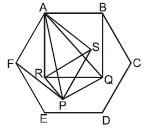
length of AP and AQ is

as these are diagonals of square with side 1.
Since AP and AQ are diagonals of square ASPF and ABQR respectively

Also, due to hexagon property, angle between adjacent sides is

, so
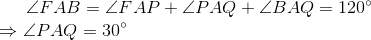
Now, consider triangle RAS.

Similarly other angles can be proved to be equal and this triangle RAS is an equilateral triangle. So, RS = AS = SP = 1.
Now, in triangle RSP,
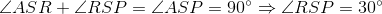
Hope the steps are clear to you. In future, I would suggest if something is not clear in the solution, please specify what exactly you were not able to understand so that We can provide answers that can help in a better way. Cheers!






 = length of AQ.
= length of AQ.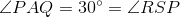
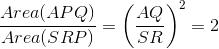

 , so
, so