Parallel and Sequential Reactions

Table of Content

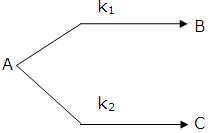
Parallel or Competing Reaction
Example of Parallel Reactions
Consecutive or Sequential Reactions
Example of Sequential Reactions
Related Resources

Parallel or Competing Reaction

The reactions in which a substance reacts or decomposes in more than one way are called parallel or side reactions.

If we assume that both of them are first order, we get.

$-\frac{d[A]}{dt} = (k_1 +k_2) [A] =k_{av}[A]$

k₁ = fractional yield of B × k_av

k₂ = fractional yield of C × k_av

If k₁ > k₂ then

A → B main and

A → C is side reaction

Let after a definite interval x mol/litre of B and y mol/litre of C are formed.

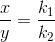
$\frac{x}{y} =\frac{k_1}{k_2}$

i.e

$\frac{\frac{d[B]}{dt}}{\frac{d[C]}{dt}} =\frac{k_1}{k_2}$

This means that irrespective of how much time is elapsed, the ratio of concentration of B to that of C from the start (assuming no B and C in the beginning ) is a constant equal to k₁/k₂.

Refer to the following video for parallel reactions:

Example of Parallel Reactions

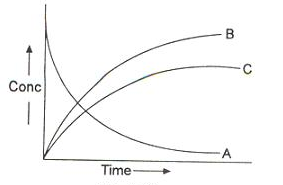
Consecutive or Sequential Reactions

This reaction is defined as that reaction which proceeds from reactants to final products through one or more intermediate stages. The overall reaction is a result of several successive or consecutive steps.

A → B → C and so on

Example of Sequential Reactions

Decomposition of ethylene oxide

(CH₂)₂O $\overset{k_1}{\rightarrow}$ CH₃CHO

CH₃CHO $\overset{k_2}{\rightarrow}$ CO + CH₄

The pyrolysis of acetone

(CH₃)₂CO $\overset{k_1}{\rightarrow}$ CH₄ + CH₂ =C=O

CH₂ =C=O $\overset{k_2}{\rightarrow}$ C₂H₄ + CO

For the reaction

$A\overset{k_1}{\rightarrow}B\overset{K_2}{\rightarrow}C$

$-\frac{d[A]}{dt} = k_1[A]$ …....(i)

$\frac{d[B]}{dt} = k_1[A]-K_2[B]$ …......(ii)

$\frac{d[C]}{dt} = k_2[B]$ ….......(iii)

Integrating equation (i), we get

$[A]-[A]_oe^{-k_1t}$

Now we shall integrate equation (ii) and find the concentration of B related to time t.

Integration of the above equation is not possible as we are not able to separate the two variables, [B] and t. Therefore we multiply equation (4) by an integrating factor $e^{-k_1t}$ , on both the sides of the equation.

Integrating with in the limits 0 to t.

Now in order to find [C], substitute equation (vi) in equation (iii), we get

B_max and t_max:

We can also attempt to find the time when [B] becomes maximum. For this we differentiate equation (vi) and find d[B]/dt & equate it to zero.

Substituting equation (vii) in equation (vi)

Question 1:

Parallel reactions take place in

a. more than one way

b. more than one step

c. in one way but more than one step

d. in one step but more than one way

Question 2:

Sequential reactions have

a. more than one way to proceed toward product

b. more than one step

c. no intermediate

d. catalyst

Question 3:

Which one of the following statements is correct?

a. parallel reactions are also known as consecutive reactions

b. Competingreactions have more than one step

c. Sequential reactions are also called consecutive reactions

d. Consecutive reactions do not have intermediates.

Question 4:

Decomposition of ethylene oxide is

a. parallel reaction

b. competing reaction

c.both parallel as well as competing reaction

d. sequential reaction

Q.1	Q.2	Q.3	Q.4
a	b	c	d

Related Resources

Click here to get detailed Syllabus of IIT JEE
Refer to the Books of Chemistry for IIT JEE
You can also refer Zero Order Reaction

To read more, Buy study materials of Chemical Kinetics comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.