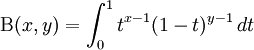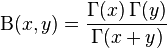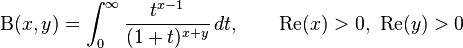Other Related Questions on integral calculus

The area of a square field is 640000cm2.what is its area in hectares
The area of a square field is 640000cm2.what is its area in hectares
integral calculus
1 Answer Available
Last Activity: 3 Years ago

Please solve this integration. I am facing difficulty in it How to solve this. Please solve anyone. Humble request
Please solve this integration. I am facing difficulty in it
How to solve this. Please solve anyone. Humble request
integral calculus
1 Answer Available
Last Activity: 3 Years ago

Using laplace transform, solve d2y/dt2 + dy/dt = t2 +2t given that y=4 and y’=-2 and t=0
Using laplace transform, solve d2y/dt2 + dy/dt = t2 +2t given that y=4 and y’=-2 and t=0
integral calculus
1 Answer Available
Last Activity: 3 Years ago

If 4th term of an A.p is zero, show that the 8th term is double the 6th term
If 4th term of an A.p is zero, show that the 8th term is double the 6th term
integral calculus
1 Answer Available
Last Activity: 3 Years ago