Hi
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits.
Kirchhoff's current law (KCL)
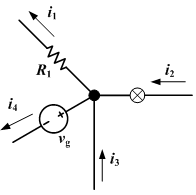
The current entering any junction is equal to the current leaving that junction. i1 + i4 = i2 + i3
This law is also called Kirchhoff's point rule, Kirchhoff's junction rule (or nodal rule), and Kirchhoff's first rule.
The principle of conservation of electric charge implies that:
- At any point in an electrical circuit that does not represent a capacitor plate, the sum of currents flowing towards that point is equal to the sum of currents flowing away from that point.
Adopting the convention that every current flowing towards the point is positive and that every current flowing away is negative (or the other way around), this principle can be stated as:
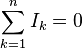
n is the total number of currents flowing towards or away from the point.
This formula is also valid for complex currents:
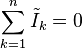
This law is based on the conservation of charge whereby the charge (measured in coulombs) is the product of the current (in amps) and the time (which is measured in seconds).
Kirchhoff's voltage law (KVL)
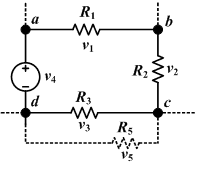
The sum of all the voltages around the loop is equal to zero. v1 + v2 + v3 + v4 = 0
This law is also called Kirchhoff's second law, Kirchhoff's loop (or mesh) rule, and Kirchhoff's second rule.
- The directed sum of the electrical potential differences around any closed circuit must be zero.
Similarly to KCL, it can be stated as:

Here, n is the total number of voltages measured. The voltages may also be complex:
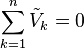
This law is based on the conservation of energy whereby voltage is defined as the energy per unit charge. The total amount of energy gained per unit charge must equal the amount of energy lost per unit charge. This seems to be true as the conservation of energy states that energy cannot be created or destroyed; it can only be transformed into one form to another.




