The omega constant is a mathematical constant defined by

It is the value of W(1) where W is Lambert's W function. The name is derived from the alternate name for Lambert's W function, the omega function.
The value of Ω is approximately 0.5671432904097838729999686622... It has properties that

or equivalently,

One can calculate Ω iteratively, by starting with an initial guess Ω0, and considering the sequence

This sequence will converge towards Ω as n→∞. This convergence is due to the fact that Ω is an attractive fixed point of the function e−x.
It is much more efficient to use the iteration

because the function

has the same fixed point but features a zero derivative at this fixed point, therefore the convergence is quadratic (the number of correct digits is roughly doubled with each iteration).
A beautiful identity due to Victor Adamchik is given by the relationship

«»[1]==Irrationality and transcendence==
Ω can be proven irrational from the fact that e is transcendental; if Ω were rational, then there would exist integers p and q such that
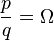
so that

![e = \left( \frac{q}{p} \right)^{\left( \frac{q}{p} \right)} = \sqrt[p]{\frac{q^q}{p^q}}](https://upload.wikimedia.org/math/e/7/e/e7eb9b5615101c77712e2bed2f28d5ea.png)
and e would therefore be algebraic of degree p. However e is transcendental, so Ω must be irrational.
Ω is in fact transcendental as the direct consequence of Lindemann–Weierstrass theorem. If Ω were algebraic, e-Ω would be transcendental; but Ω=exp(-Ω), so these cannot both be true.
….….….….…..if you like my advise just click on approve button ...and please type for any other quary if you have,,,,,,,,,,,,,,,,,,,

















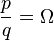

![e = \left( \frac{q}{p} \right)^{\left( \frac{q}{p} \right)} = \sqrt[p]{\frac{q^q}{p^q}}](https://upload.wikimedia.org/math/e/7/e/e7eb9b5615101c77712e2bed2f28d5ea.png)




