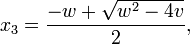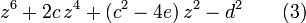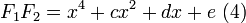Algebra> quartic-equation...
Algebra> quartic-equation...

 8 Answers
8 AnswersShivam Dimri
you need practise for it!!!
the other formula -b +- ....
is still available..
Akash Kumar Dutta
its very easy
first method is by discriminant ..whichtells us the nature of the roots,
and after that apply graphical method which tells us about their signs.
nihit kumar
i think you know how to take out descrimnant. aftr you get it check the value of d if, d=o then it is real and equal or if d>0 then it is unequal and real and f d<0 then i is imaginary.
shiddhant bhattacharya
Solving a quartic equation
The 4 roots ( ) for any quartic equation;
) for any quartic equation;
where  are equal to those of
are equal to those of
where  ,
,  ,
,  and
and 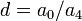 .
.
The roots in terms of these 4 coefficients are given by the formula in the image below:
However, this formula is too unwieldy for general use, hence other methods or simpler formulas (given below) are generally used.[7]
[edit]Special cases
Consider the quartic
[edit]Degenerate case
If a0 = 0 then Q(0) = 0, and so x = 0 is a solution. It follows that Q(x) may be factorised as Q(x) = x·(a4x3 + a3x2 + a2x + a1). The remaining three roots (see Fundamental Theorem of Algebra) can be found by solving the cubic equation a4x3 + a3x2 + a2x + a1 = 0.
[edit]Evident roots: 1 and −1 and −k
If 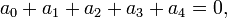 then
then 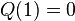 , so
, so  is a root. Similarly, if
is a root. Similarly, if 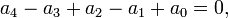 that is,
that is,  then
then  is a root.
is a root.
When  is a root, we can divide
is a root, we can divide  by
by  and get
and get
where  is a cubic polynomial, which may be solved to find
is a cubic polynomial, which may be solved to find 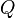 ''s other roots. Similarly, if
''s other roots. Similarly, if  is a root,
is a root,
where  is some cubic polynomial.
is some cubic polynomial.
If  then −k is a root and we can factor out
then −k is a root and we can factor out 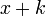 ,
,
And if  then both
then both  and
and 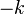 are roots Now we can factor out
are roots Now we can factor out  and get
and get
To get Q ''s other roots, we simply solve the quadratic factor.
[edit]Biquadratic equations
If  then
then
We call such a polynomial a biquadratic, which is easy to solve.
Let 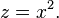 Then Q becomes a quadratic q in
Then Q becomes a quadratic q in 
Let  and
and  be the roots of q. Then the roots of our quartic Q are
be the roots of q. Then the roots of our quartic Q are
[edit]Quasi-symmetric equations
Steps:
- Divide by x 2.
- Use variable change z = x + m/x.
[edit]The general case, along Ferrari''s lines
To begin, the quartic must first be converted to a depressed quartic.
[edit]Converting to a depressed quartic
Let
be the general quartic equation we want to solve. Divide both sides by A to produce a monic polynomial,
The first step should be to eliminate the x3 term. To do this, change variables from x to u, such that
 .
.
Then
Expanding the powers of the binomials produces
Collecting the same powers of u yields
Now rename the coefficients of u. Let
The resulting equation is
which is a depressed quartic equation.
If  then we have a biquadratic equation, which (as explained above) is easily solved; using reverse substitution we can find our values for
then we have a biquadratic equation, which (as explained above) is easily solved; using reverse substitution we can find our values for  .
.
If  then one of the roots is
then one of the roots is  and the other roots can be found by dividing by
and the other roots can be found by dividing by  , and solving the resulting depressed cubic equation,
, and solving the resulting depressed cubic equation,
Using reverse substitution we can find our values for  .
.
[edit]Ferrari''s solution
Otherwise, the depressed quartic can be solved by means of a method discovered by Lodovico Ferrari. Once the depressed quartic has been obtained, the next step is to add the valid identity
to equation (1), yielding
The effect has been to fold up the u4 term into a perfect square: (u2 + α)2. The second term, αu2 did not disappear, but its sign has changed and it has been moved to the right side.
The next step is to insert a variable y into the perfect square on the left side of equation (2), and a corresponding 2y into the coefficient of u2 in the right side. To accomplish these insertions, the following valid formulas will be added to equation (2),
and
These two formulas, added together, produce
which added to equation (2) produces
This is equivalent to
The objective now is to choose a value for y such that the right side of equation (3) becomes a perfect square. This can be done by letting the discriminant of the quadratic function become zero. To explain this, first expand a perfect square so that it equals a quadratic function:
The quadratic function on the right side has three coefficients. It can be verified that squaring the second coefficient and then subtracting four times the product of the first and third coefficients yields zero:
Therefore to make the right side of equation (3) into a perfect square, the following equation must be solved:
Multiply the binomial with the polynomial,
Divide both sides by −4, and move the −β2/4 to the right,
This is a cubic equation for y. Divide both sides by 2,
[edit]Conversion of the nested cubic into a depressed cubic
Equation (4) is a cubic equation nested within the quartic equation. It must be solved to solve the quartic. To solve the cubic, first transform it into a depressed cubic by means of the substitution
Equation (4) becomes
Expand the powers of the binomials,
Distribute, collect like powers of v, and cancel out the pair of v2 terms,
This is a depressed cubic equation.
Relabel its coefficients,
The depressed cubic now is
[edit]Solving the nested depressed cubic
The solutions (any solution will do, so pick any of the three complex roots) of equation (5) are computed as (see Cubic equation)
where
and V is computed according to the two defining equations  and
and  , so
, so
[edit]Folding the second perfect square
With the value for y given by equation (6), it is now known that the right side of equation (3) is a perfect square of the form
![(s^2)u^2+(2st)u+(t^2) = (s^2)\left(u - {-(2st) \over 2(s^2)}\right)^2=\left[\sqrt{(s^2)}\left(u - {-(2st) \over 2(s^2)}\right)\right]^2,](http://upload.wikimedia.org/math/2/f/8/2f87c090a98031bbc2aa251c3d0a30fd.png)

- (This is correct for both signs of square root, as long as the same sign is taken for both square roots. A ± is redundant, as it would be absorbed by another ± a few equations further down this page.)
so that it can be folded:
 .
.- Note: If β ≠ 0 then α + 2y ≠ 0. If β = 0 then this would be a biquadratic equation, which we solved earlier.
Therefore equation (3) becomes
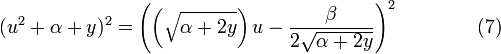 .
.
Equation (7) has a pair of folded perfect squares, one on each side of the equation. The two perfect squares balance each other.
If two squares are equal, then the sides of the two squares are also equal, as shown by:
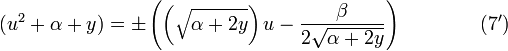 .
.
Collecting like powers of u produces
 .
.- Note: The subscript s of
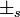 and
and  is to note that they are dependent.
is to note that they are dependent.
- Note: The subscript s of
Equation (8) is a quadratic equation for u. Its solution is
Simplifying, one gets
This is the solution of the depressed quartic, therefore the solutions of the original quartic equation are

- Remember: The two
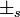 come from the same place in equation (7''), and should both have the same sign, while the sign of
come from the same place in equation (7''), and should both have the same sign, while the sign of 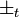 is independent.
is independent.
- Remember: The two
[edit]Summary of Ferrari''s method
Given the quartic equation
its solution can be found by means of the following calculations:
If  then
then
Otherwise, continue with
(either sign of the square root will do)
(there are 3 complex roots, any one of them will do)
As stated above, Cardano credited Ferrari as the first to discover one of these labyrinthine solutions. The equation he solved was:
which was already in depressed form. It has a pair of solutions that can be found with the set of formulas shown above.
[edit]Ferrari''s solution in the special case of real coefficients
If the coefficients of the quartic equation are real then the nested depressed cubic equation (5) also has real coefficients, thus it has at least one real root.
Furthermore the cubic function  where P and Q are given by (5) has the properties that
where P and Q are given by (5) has the properties that
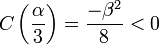 and
and
 where α and β are given by (1).
where α and β are given by (1).
This means that (5) has a real root greater than  , and therefore that (4) has a real root greater than
, and therefore that (4) has a real root greater than  .
.
Using this root the term  in (8) is always real, which ensures that the two quadratic equations (8) have real coefficients.[8]
in (8) is always real, which ensures that the two quadratic equations (8) have real coefficients.[8]
[edit]Obtaining alternative solutions by factoring out complex conjugate solutions
It could happen that one only obtained one solution through the seven formulae above, because not all four sign patterns are tried for four solutions, and the solution obtained is complex. It may also be the case that one is only looking for a real solution. Let x1 denote the complex solution. If all the original coefficients A, B, C, D and E are real — which should be the case when one desires only real solutions — then there is another complex solution x2, which is the complex conjugate of x1. If the other two roots are denoted as x3 and x4 then the quartic equation can be expressed as
but this quartic equation is equivalent to the product of two quadratic equations:
and
Since
then
Let
so that equation (9) becomes
Also let there be (unknown) variables w and v such that equation (10) becomes
Multiplying equations (11) and (12) produces
Comparing equation (13) to the original quartic equation, it can be seen that
and
Therefore
Equation (12) can be solved for x yielding
These two solutions are the desired real solutions if real solutions exist.
[edit]Alternative methods
[edit]Factorization into quadratics
One can solve a quartic by factoring it into a product of two quadratics.[9] Let
By equating coefficients, this results in the following set of simultaneous equations:
This can be simplified by starting again with a depressed quartic where 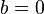 , which can be obtained by substituting
, which can be obtained by substituting  for
for  , then
, then  , and:
, and:
It''s now easy to eliminate both  and
and  by doing the following:
by doing the following:
If we set  , then this equation turns into the resolvent cubic equation
, then this equation turns into the resolvent cubic equation
which is solved elsewhere. Then:
The symmetries in this solution are easy to see. There are three roots of the cubic, corresponding to the three ways that a quartic can be factored into two quadratics, and choosing positive or negative values of  for the square root of
for the square root of 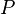 merely exchanges the two quadratics with one another.
merely exchanges the two quadratics with one another.
The above solution shows that the quartic polynomial with a zero coefficient on the cubic term is factorable into quadratics with rational coefficients if and only if the resolvent cubic  has a root which is the square of a rational; this can readily be checked using the rational root test.
has a root which is the square of a rational; this can readily be checked using the rational root test.
[edit]Galois theory and factorization
The symmetric group S4 on four elements has the Klein four-group as a normal subgroup. This suggests using a resolvent cubic whose roots may be variously described as a discrete Fourier transform or aHadamard matrix transform of the roots; see Lagrange resolvents for the general method. Suppose ri for i from 0 to 3 are roots of
If we now set
then since the transformation is an involution we may express the roots in terms of the four si in exactly the same way. Since we know the value s0 = -b/2, we really only need the values for s1, s2 and s3. These we may find by expanding the polynomial
which if we make the simplifying assumption that b=0, is equal to
This polynomial is of degree six, but only of degree three in z2, and so the corresponding equation is solvable. By trial we can determine which three roots are the correct ones, and hence find the solutions of the quartic.
We can remove any requirement for trial by using a root of the same resolvent polynomial for factoring; if w is any root of (3), and if
then
We therefore can solve the quartic by solving for w and then solving for the roots of the two factors using the quadratic formula.
[edit]Algebraic geometry
An alternative solution using algebraic geometry is given in (Faucette 1996), and proceeds as follows (more detailed discussion in reference). In brief, one interprets the roots as the intersection of two quadratic curves, then finds the three reducible quadratic curves (pairs of lines) that pass through these points (this corresponds to the resolvent cubic, the pairs of lines being the Lagrange resolvents), and then use these linear equations to solve the quadratic.
The four roots of the depressed quartic  may also be expressed as the x coordinates of the intersections of the two quadratic equations
may also be expressed as the x coordinates of the intersections of the two quadratic equations 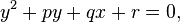
 i.e., using the substitution
i.e., using the substitution 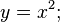 that two quadratics intersect in four points is an instance of Bézout''s theorem. Explicitly, the four points are
that two quadratics intersect in four points is an instance of Bézout''s theorem. Explicitly, the four points are  for the four roots
for the four roots 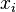 of the quartic.
of the quartic.
These four points are not collinear because they lie on the irreducible quadratic 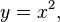 and thus there is a 1-parameter family of quadratics (a pencil of curves) passing through these points. Writing the projectivization of the two quadratics as quadratic forms in three variables:
and thus there is a 1-parameter family of quadratics (a pencil of curves) passing through these points. Writing the projectivization of the two quadratics as quadratic forms in three variables:
the pencil is given by the forms  for any point
for any point ![[\lambda,\mu]](http://upload.wikimedia.org/math/b/1/6/b16ebd8e960e372d25f91f1f4f7bcd27.png) in the projective line – in other words, where
in the projective line – in other words, where  and
and  are not both zero, and multiplying a quadratic form by a constant does not change its quadratic curve of zeros.
are not both zero, and multiplying a quadratic form by a constant does not change its quadratic curve of zeros.
This pencil contains three reducible quadratics, each corresponding to a pair of lines, each passing through two of the four points, which can be done  different ways. Denote these
different ways. Denote these 

 Given any two of these, their intersection is exactly the four points.
Given any two of these, their intersection is exactly the four points.
The reducible quadratics, in turn, may be determined by expressing the quadratic form  as a 3×3 matrix: reducible quadratics correspond to this matrix being singular, which is equivalent to its determinant being zero, and the determinant is a homogeneous degree three polynomial in
as a 3×3 matrix: reducible quadratics correspond to this matrix being singular, which is equivalent to its determinant being zero, and the determinant is a homogeneous degree three polynomial in  and
and 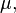 and corresponds to the resolvent cubic.
and corresponds to the resolvent cubic.
or instead u could go to this website and chk it out urself...
http://en.wikipedia.org/wiki/Quartic_function#Solving_a_quartic_equation
A. Srikar
if the equation is ax^2+bx+c=0 , then if b^2-4ac>o , roots are real & distinct......
if b^2-4ac =0 , then roots are real & equal..
if b^2-4ac<0 , then roots are complex & conjugate & distinct to each other....
D Som
are they both real? are they both imaginary?
Are they irrational?
take ax2+bx+c=0
check (b2-4ac)<>=0 depending on that you will get answers to above questions.
Rember if one root is imaginary that the other is its conjugate. If one root is irrational then the other is also.
Rohan Das
you can use two things.either descartes rule of signs or discriminant
BHOOPELLY SAIKUMAR

LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.

Full Live Access

Study Material

Live Doubts Solving

Daily Class Assignments
Other Related Questions on algebra


Can we divide two vectors? If this is possible then how?
algebra
Last Activity: 1 Year ago

How do you write “the product of 18 and q” as an algebraic expression?
algebra
Last Activity: 1 Year ago

दहावीच्या आय सी एस इ विद्यार्थ्यांनी पुढे काय करायला पाहिजे
algebra
Last Activity: 3 Years ago







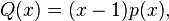




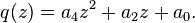






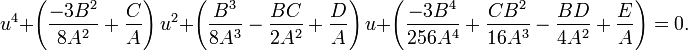
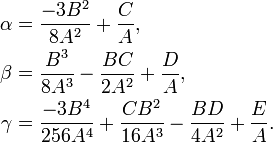
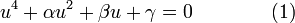
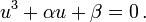




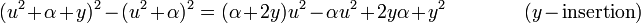





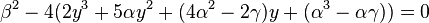



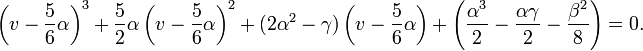



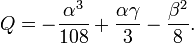

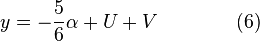
![U=\sqrt[3]{-{Q\over 2}\pm \sqrt{{Q^{2}\over 4}+{P^{3}\over 27}}}](http://upload.wikimedia.org/math/b/6/f/b6f987f2ebbf25dc28f768e5138e1363.png)
![V=\begin{cases} -\frac{P}{3U}&\text{ if }U\ne 0\text{ and }\\ -\sqrt[3]{Q}&\text{ if }U=0\ . \end{cases}](http://upload.wikimedia.org/math/a/6/f/a6f2ffb5408554862e1e2da2dd6192f3.png)
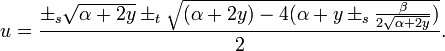








![U = \sqrt[3]{R},](http://upload.wikimedia.org/math/e/3/3/e3322597c0d374ee70164f962ea53329.png)
![y = \begin{cases} - {5 \over 6} \alpha + U - \frac{P}{3U} & \text{if }U\ne 0\\ -{5\over 6} \alpha - \sqrt[3]{Q} & \text{if }U=0 \end{cases}](http://upload.wikimedia.org/math/1/e/5/1e516f83855ee18458fa3f0055dcb000.png)







![\begin{matrix} (x-x_1)(x-x_2)&=&x^2-(x_1+x_1^\star)x+x_1x_1^\star\qquad\qquad\qquad\quad \\ &=&x^2-2\,\mathrm{Re}(x_1)x+[\mathrm{Re}(x_1)]^2+[\mathrm{Im}(x_1)]^2. \end{matrix}](http://upload.wikimedia.org/math/4/4/a/44a486189cc52f48c6d3487926282b6d.png)

![b = \left[ \mathrm{Re}( x_1) \right]^{2} + \left[ \mathrm{Im}(x_1) \right]^{2}](http://upload.wikimedia.org/math/9/c/0/9c0f7d72f03a6d901ce5a55d7afdbcb0.png)


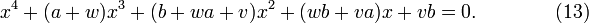
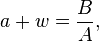




![v = {E \over A b} = {E \over A \left( [ \mathrm{Re}(x_1) ]^2 + [ \mathrm{Im}(x_1) ]^2 \right) }.](http://upload.wikimedia.org/math/3/4/7/347b3acbe99d2f51ec309a6dfbc503f0.png)