Dear Student,
Suppose Houses are ABCDE and corresponding letters are ABCDE.
So the total no of correct probabilities are :
ABECD, AECBD and so on..
And total no of possibilities are :5!
A derangement is a permutation in which none of the objects appear in their "natural" (i.e., ordered) place. For example, the only derangements of 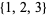 are
are 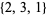 and
and 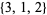 , so
, so 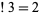 . Similarly, the derangements of
. Similarly, the derangements of 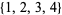 are
are 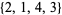 ,
, 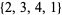 ,
, 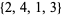 ,
, 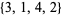 ,
, 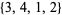 ,
, 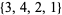 ,
, 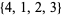 ,
, 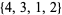 , and
, and 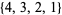 . Derangements are permutations without fixed points (i.e., having no cycles of length one). The derangements of a list of
. Derangements are permutations without fixed points (i.e., having no cycles of length one). The derangements of a list of 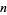 elements can be computed using Derangements[n] in the Mathematica package Combinatorica` .
elements can be computed using Derangements[n] in the Mathematica package Combinatorica` .
The problem was formulated by P. R. de Montmort in 1708, and solved by him in 1713 (de Montmort 1713-1714). Nicholas Bernoulli also solved the problem using the inclusion-exclusion principle (de Montmort 1713-1714, p. 301; Bhatnagar 1995, p. 8).
Derangements are also called rencontres numbers (named after rencontres solitaire) or complete permutations, and the number of derangements 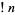 on
on 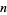 elements is called the subfactorial of
elements is called the subfactorial of 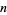 .
.
The function giving the number of distinct derangements on 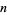 elements is called the subfactorial
elements is called the subfactorial 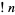 and is equal to
and is equal to
(Bhatnagar 1995, pp. 8-9), where 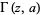 is the incomplete gamma function, or
is the incomplete gamma function, or
![!n=[(n!)/e],](http://mathworld.wolfram.com/images/equations/Derangement/NumberedEquation1.gif) |
(3)
|
where 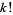 is the usual factorial and
is the usual factorial and ![[x]](http://mathworld.wolfram.com/images/equations/Derangement/Inline29.gif) is the nearest integer function.
is the nearest integer function.
Cracking IIT just got more exciting,It s not just all about getting assistance from IITians, alongside Target Achievement and Rewards play an important role. ASKIITIANS has it all for you, wherein you get assistance only from IITians for your preparation and win by answering queries in the discussion forums. Reward points 5 + 15 for all those who upload their pic and download the ASKIITIANS Toolbar, just a simple to download the toolbar….
So start the brain storming…. become a leader with Elite Expert League ASKIITIANS
Thanks
Aman Bansal
Askiitian Expert














