Addition and Subtraction of Vectors

Scalar quantities can be added algebraically. for example, 4 kg of sugar and 3 kg of sugar, when combined together in any way, always give 7 kg of sugar. This is not always there in case of vectors, since they possess directions, also, in addition to the magnitudes.

Following are the some points regarding vector addition:

(a) Addition or composition of vectors means finding the resultant of a number of vectors acting on a body.

(b) The vectors can be added geometrically and not algebraically.

(c) Vectors, whose resultant is to be calculated behave independent of each other. In other words, each vector behaves as if the other vectors were absent.

(d) Vector addition is commutative.

So, 

It means that the law of addition of vectors is independent of the order of vectors.

Graphical Representation of Vector Addition

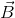To find  , shift  vector  such that its initial point coincides with the terminal point of vector 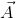. Now, the vector whose initial point coincides with the initial point of vector  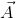, and terminal point coincides with the terminal point of vector  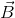 represents  as shown in the above figure. 

To find , shift 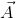 such that its initial point coincides with the terminal point 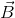. A vector whose initial point coincides with the initial point of  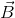and terminal point coincides with the terminal point of  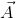represents .

                        

Triangle’s Law of Vector Addition

It is a law for the addition of two vectors. It can be stated as follows:

“If two vectors are represented (in magnitude and direction) by the two sides of a triangle, taken in the same order, then their resultant in represented (in magnitude and direction) by the third side of the triangle taken in opposite order.”

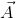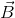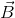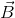Consider two vectors  and  [Below Figure] acting, simultaneously, on a body. Represent vector  by the line . At A draw another line  representing . Join OC. Then  (=) gives the resultant of 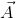  and 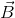. It can be noted that   and  are in same order while  is in opposite order. This is in accordance with the triangle’s law.

So,  = 

         =  + 

        = +

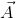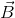
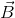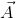
It is, further, clear that the order of vectors in vector addition is immaterial. So, vector addition is commutative. 

If θ is the angle between 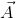 and 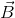, then the magnitude of the resultant vector  will be,

R = √(A²+ B² )+ 2AB cos θ

and

if ? is the angle between 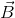 and  then,

? = tan^-1 [A sinθ/(B+A cosθ)]  

If three vectors acting, simultaneously, on a particle can be represented by the three sides of a triangle taken in the same order, then the particle will remain in equilibrium. 

Mathematically, it can be expressed as follows:

Law of Parallelogram of Vectors

The addition of two vectors may also be understood by the law of parallelogram. It states that “if two vectors acting simultaneously at a point are represented in magnitude and direction by the two sides of a parallelogram drawn from a point, their resultant is given in magnitude and direction by the diagonal of the parallelogram passing through that point.”

According to this law if two vectors  and   are represented by two adjacent sides of a parallelogram both pointing outwards as shown in the figure below , then the diagonal drawn through the intersection of the two vectors represents the resultant (i.e. vector sum of  and  ). If Q is displacement from position AD to BC by displacing it parallel to itself, this method becomes equivalent to the triangle method. 

                               

In case of addition of two vectors by parallelogram method as shown in figure, the magnitude of resultant will be given by, 

                                       (AC)² = (AE)² + (EC)² 

                               or R² = (P + Q cos θ)² (Q sin θ)²

                               or R = √(P²+ Q² )+ 2PQcos θ 

And the direction of resultant from vector P will be given by
 
                              tan ? = CE/AE = Qsinθ/(P+Qcosθ) 

                                  ? = tan^-1 [Qsinθ/(P+Qcosθ)]  

Special Cases

(a) When  θ = 0°, cos θ = 1 , sin θ = 0°

Substituting for cos θ in equation R = √(P²+ Q² )+ 2PQcos θ, we get,

R = √(P²+ Q² )+ 2PQcos θ

   = √(P+ Q)²

or R = P+Q (maximum)

Substituting for sin θ  and cos θ  in equation ? = tan-1 [Qsinθ/(P+Qcosθ)], we get,

? = tan^-1 [Qsinθ/(P+Qcosθ)]  

   = tan^-1 [(Q×0)/(P+(Q×1))]

  = tan^-1(0)

 = 0°

The resultant of two vectors acting in the same directions is equal to the sum of the two. The direction of resultant coincides with those of the two vectors.

(b) When  θ = 180°, cos θ = -1 , sin θ = 0°

Substituting for cos θ in equation R = √(P²+ Q² )+ 2PQcos θ, we get,

R = √(P²+ Q² )+ 2PQ(-1)

  =√P²+ Q² – 2PQ

   = √(P –  Q)² (minimum)

R = P – Q (minimum)

Substituting for sin θ  and cos θ  in equation ? = tan-1 [Qsinθ/(P+Qcosθ)], we get,

? = tan^-1 [Qsinθ/(P+Qcosθ)]  

   = tan^-1 [(Q×0)/(P+(Q×(-1)))]

  = tan^-1(0)

 = 0°

This magnitude of the resultant of two vectors acting in opposite direction is equal to the difference of magnitudes of the two and represents the minimum value. The direction of the resultant is in the direction of the bigger one.

 (c) When  θ = 90°, cos θ = 0 , sin θ = 1

Substituting for cos θ in equation R = √(P²+ Q² )+ 2PQcos θ, we get,

R = √(P²+ Q² )+ (2PQ×0)

   = √P²+ Q² 

Substituting for sin θ  and cos θ  in equation ? = tan-1 [Qsinθ/(P+Qcosθ)], we get,

? = tan^-1 [Qsinθ/(P+Qcosθ)]  

   = tan^-1 [(Q×1)/(P+(Q×(0)))] 

  = tan^-1(Q/P)

The resultant of two vectors acting at right angles to each other is equal to the square root of the sum of the squares of the magnitudes of the two vectors. Direction of the resultant depends upon their relative magnitudes. 

Vector Subtraction

The process of subtracting one vector from another is equivalent to adding, vectorially, the negative of the vector to be subtracted. Suppose there are two vectors 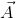 and 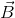, shown in figure (A) and we have to subtract  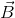and 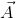. It is just the same thing as adding vectors –  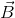to 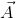. The resultant is shown in figure (B). 

                                    
                                              Figure (A) 

                                         
                                              Figure (B) 

           
Properties of Vector Addition:-  Vector addition obeys the following properties.

1. Vector addition is commutative:- It means that the order of vectors to be added together does not affect the result of addition. If two vectors 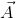 and 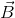 are to be added together, then

       
                  
                                         
     2. Vector addition is associative:- While adding three or more vectors together, the mutual grouping of vector does not affect the result.

           Mathematically,

  3. Vector addition is distributive:- It means a scalar times the sum of two vectors is equal to the sum of the scalar times of the two vectors, individually.

      Mathematically,

Geometrical Representation of Addition  of Vectors

                                     
Magnitude and direction of :-
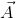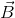Let angle between vector  and  be θ.
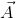In the figure vector () = vector  , vector () = vector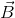 
From Δ ADB,

                                 AD = b cos θ
                                  BD = b sin θ

                               
In right angled ΔODB,

                      OD = a + b cosθ
                     BD = b sin θ

                    Therefore, OB = √(OD²+BD² )
                    => |a +b |=√(a²+b²+2ab cos θ)
                   |a +b |_max   =  a+b   when θ = 2nπ

                   |a +b |_min   =  |a – b|   when θ = (2n + 1)π
                                       (where n = 0, 1, 2, …..)
If a + b  is inclined at an angle α with vector a , then
tan α = ((b sin θ)/(a+b cosθ))

Related Resources

• Click here for the Detailed Syllabus of IIT JEE Physics.

• Look into the Sample Papers of Previous Years to get a hint of the kinds of questions asked in the exam.

• You can get the knowledge of Useful Books of Physics.

To read more, Buy study materials of Units & Dimensions comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here.