Geometrical Representation of Fundamental Operations

The various fundamental laws can be represented graphically. The graphical representation makes it easier to understand the laws. The four fundamental laws of geometry have been explained below:

(i) Geometrical Representation of Addition:

If two points P and Q represent complex numbers z₁ and z₂ respectively in the Argand Plane, then the sum z₁+z₂ is represented by the extremity R of the diagonal OR of parallelogram OPRQ having OP and OQ as two adjacent sides. The addition of the complex numbers z₁ and z₂ can be assumed to be the addition of the vectors by utilizing the parallelogram law.

(ii) Geometrical representation of subtraction:

The representation of the difference of two complex numbers is slightly complicated than the addition of the complex numbers. The easiest way of presenting the subtraction is to think of addition of a negative vector. If we want to represent z₁-z₂, then the easiest way of representing it would be to think of adding a negative vector z₁ + (-z₂). The negative vector is the same as the positive one, the only difference being that the negative vector points in the opposite direction.

The difference vector z₁ - z₂ is represented below

Remark: It is important to note here that the vector representing the difference of the vectors z₁ - z₂ may also be drawn joining the end point of z₂ to the tip of z₁ instead of the origin. This kind of representation does not alter the meaning or interpretation of the difference operator. The difference operator joining the tips of z₁ and z₂ is represented below:

(iii) Modulus and argument of multiplication of two complex numbers: Modulus and argument are two extremely important concepts associated with complex numbers. 

Modulus of a complex number: The modulus of a complex number is defined to be the distance of the number from the origin. It is denoted by |z| and the value of the modulus of z = x+iy is √x²+y².

Argument of a complex Number: Argument of a complex number is basically the angle that explains the direction of the complex number. It is measured in radians. If we have the complex number in polar form i.e. z = r(cos θ + i sin θ), then its argument is θ. 

Modulus of product of two complex numbers: Let z₁ and z₂ be two complex numbers in polar form

z₁ = r₁(cos θ₁ + i sin θ₁)

z₂ = r₂(cos θ₂ + i sin θ₂)

Hence their product is given by

z₁z₂ = r₁r₂ [(cos θ₁ cos θ₂ – sin θ₁ sin θ₂) + i(sin θ₁ cos θ₂ + cos θ₁ sin θ₂)].

This expression can be further simplified as

z₁z₂ = r₁r₂ [(cos (θ₁ + θ₂) + i sin (θ₁ + θ₂)].

The product z₁z₂ has the modulus r₁r₂ and the argument (θ₁ + θ₂).

Theorem: For any two complex numbers z₁, z₂

We have, |z₁, z₂| = |z₁| |z₂| and arg(z₁, z₂) = arg(z₁) + arg(z₂)

Proof: z₁ = r₁ e^iθ1, z₂ = r₂ e^iθ2

        z₁z₂ = r₁ r₂ e^i(θ1+θ2)

        => |z₁ z₂|=|z₁|=|z₂|

arg (z₁z₂) = arg(z₁) + arg(z₂)

i.e., to multiply two complex numbers, we multiply their absolute values and add their arguments.
 
View the following video for more on argument and modulus 

Some Key Points

(i) P.V. arg(z₁z₂) ≠ P.V. arg(z₁) + P.V. arg(z₂)

(ii) |z₁z₂ ...... z_n| = |z₁| |z₂| ......... |z_n|

(iii) arg(z₁.z₂ ......... z_n) = argz₁+argz₂+ ........ + argz_n

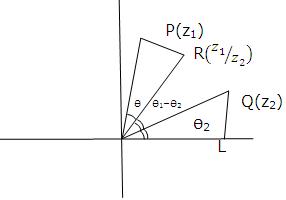
(iv) Geometrical representation of multiplication of complex numbers -

Let P, Q be represented by z₁= r₁ e^iθ1, z₂ = r₂ e^iθ2 respectively. To find point R representing complex number z₁ z₂, we take a point L on real axis such that OL=1 and draw triangle OQR similar to triangle OLP. Therefore, 

OR/OQ = OP/OL = OR = OP*OQ

i.e., OR = r₁ r₂ and ∠ QOR = θ,

R(z₁z₂) Q(z₂) P(z₁)

 ∠ LOR = ∠ LOP + ∠ POQ + ∠ QOR

           = Q₁ + Q₂ - Q₁ + Q₁

            = Q₁ + Q₂

Hence, R is represented by z₁ z₂ = r₁ r₂ e^i(Q1+Q2)

(v) Modulus and argument of division of two complex numbers:

Theorem: If z₁ and z₂ ( ≠0 ) are two complex numbers, then |z₁/z₂| =

      |z₁|/|z₂|   and arg(z₁/z₂) = arg z₁ - arg z₂

Note:        

       P.V. arg(z₁/z₂) ≠  P.V. arg (z₁) - P.V. arg (z₂)

 (vi) Geometrical representation of the division of complex numbers-

Let P, Q be represented by z₁= r₁ e^iθ1, z₂ = r₂ e^iθ2 respectively. To find point R representing complex number z₁/z₂, we tale a point L on real axis such that OL=1 and draw a triangle OPR similar to OQL.

Therefore, OP/OQ = OR/OL

 => OR = r₁/r₂

and ∠LOR = ∠LOP - ∠ROP

                = θ₁ - θ₂

Hence, R is represented by z₁/z₂ =r₁/r₂ e^{i(θ1 - θ2)}

askIITians offers comprehensive study material which covers all the topics of IIT JEE Mathematics syllabus in detail. It is important to have a strong grip on the various algebraic operators as they lay the foundation of several other topics. The JEE aspirants must master the topic in order to remain competitive in the JEE.

Related Resources

• Click here for the Entire Syllabus of IIT JEE Mathematics.

• Look into the Previous Year Papers with Solutions to get a hint of the kinds of questions asked in the exam.

• You can get the knowledge of Useful Books of Mathematics here.

To read more, Buy study materials of Complex Numbers comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.