The Back Bencher’s Tip to learn the Trigonometric Identities

All right! So, now you are planning to study the monster called trigonometry! I am sure majority of you would agree with me on this that trigonometry is a hard nut to crack! The concepts involved in it are not very hard but what makes it all the more challenging is that it is over flooded with formulae.

You learn first five formulae, reach the sixth and …. you can’t recall the first one! If this is what you are experiencing, then you are one of the numerous students suffering from the trigonometry phobia! Well, you should not be cursing yourself for this because, after all you are human with limited memory and you cannot expect your brain to be a memory card which stores everything permanently!

Don’t worry my friend, we bring you some of the interesting ways of learning these formulae and befriending the monster called trigonometry! Get ready to explore the interesting world of trigonometry!

There are certain basic concepts which you will have to learn (and we can’t really help you in that!) like periodicity of functions and Pythagorean identity. Now, let us begin our tour:

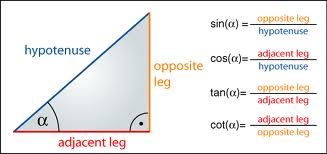
We begin with the basic trigonometric functions i.e. sin, cos and tan.
For remembering this (although, it’s too simple), write the functions in this order

sin           cos           tan
OH           AH          OA
cosec        sec           cot

So, just remember oh ah oa…. or rather you can learn it as SOH CAH TOA which says sine means OH (opposite/hypotenuse), cos means AH (adjacent side/hypotenuse), tan for OA (opposite side/adjacent side).

• Now, once you know these six basic formulae, next important point is the sign of trigonometric functions. So here comes the technique to remember the signs of trigonometric functions in various quadrants.

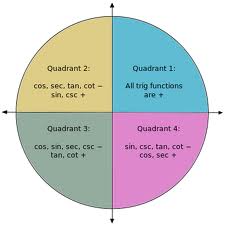We know that there are four quadrants. In the first quadrant, all trigonometric functions are positive. In the second quadrant, sine and cosec are positive and all remaining functions are negative. Similarly only tangent and cotangent are positive in the third quadrant while sec and cosec are positive in the fourth quadrant.
Students often get confused in memorizing this. This should be better remembered as After School To College or Add Sugar To Tea. The initials stand for the functions which are positive in the respective quadrants. Once you learn it this way, you are sure to remember it throughout your life without getting confused.
Next is the core of trigonometry i.e. the trigonometric identities. Frankly speaking, there is no substitute for learning the trigonometric identities. One of the options is that you can derive them using the Euler’s formula. But that is possible only if you have sufficient time. Demoivre’s theorem is also useful in this context but that also takes time. Hence, while the sad part is that one has to learn the identities as there is no other alternative, the good part is that we are here to simplify this process for you!

Consider the figure given below. This figure is called the hexagon of trigonometric identities. Some of the basic identities can be remembered with the help of this hexagon.

Reading across the central 1 diagonally gives us the reciprocal functions i.e.

cosec x = 1/sin x

sec x = 1/cos x

cot x = 1/tan x

Next, we can also derive the standard identities reading down any triangle in clockwise direction i.e.

sin²x + cos²x = 1

1 + cot²x = cosec²x

tan²x + 1 = sec²x

Hence, these basic concepts can be easily remembered with the help of this hexagon.

• We now move on to the sine and cosine laws in triangle:

In any triangle ABC having sides a, b and c, we have

1.The sine law

sin A / a = sin B / b = sin C / c

So, here you can just remember that sine of an angle divided by same side is equal to the rest of the angles divided by the corresponding sides.

2 The cosine laws

a ² = b ² + c ² – 2 bc cos A

b ² = a ² + c ² – 2 ac cos B

c ² = a ² + b ² – 2 a b cos C

We take the first one. You can learn this as one side a = (b-c)² and the 2bc term has cosine of the angle corresponding to the main side i.e. a.

• Sum and Difference Formulae:

1. sin (A ± B) = sin A cos B ± cos A sin B

First of all, remember that the formula of sin (A ± B) contains both the functions sin and cos. Now, to memorize the formula, learn “SC student studies CS (computer science)”, where SC→CS imply sin cos and then cos sin. The sign between the terms remains the same i.e. the formula for sin (A + B) will contain a positive sign in between terms and that of sin (A – B) will contain a negative sign.

2. cos (A ± B) = cos A cos B ∓ sin A sin B

This formula of cos contains both the trigonometric functions in pairs. You can learn it as Caste Conflict is a form of Social Sin i.e. CC→SS. Now this statement is in negative sign and hence the sign would be negative i.e. while computing cos (A + B), the sign between the terms is negative and vice-versa.

Once you remember this, you can easily derive the remaining formulae.

• Multiple Angle Formulae:

1. sin 2A = 2 sin A cos A

Remember that both the sides contain 2. Further you can learn it as SSC exam i.e. S→SC, which implies that sine of an angle = twice sine and cosine of half of that angle.

2. cos 2A = cos²A – sin ²A

= 1 – 2sin²A

= 2 cos²A -1

In this case, there are three formulae for cosine of 2A. But, one should try to learn just one as others can be derived from it using the relationship of sine and cosine of angles.

3. sin 3A = 3 sin A – 4sin³A

In this again, remember that every term contains 3. Secondly, all the terms contain the same trigonometric ratio i.e. sine.

4. cos 3A = 4cos³A – 3 cos A

This term is completely based on the previous formula. By just interchanging both the terms in the previous case and replacing sine by cos we obtain this formula.

• Some general tips to help you learn the identities:

1. Remember that sin x = (e^ix – e^-ix)/2i and cos x = (e^ix + e^-ix)/2 and use the exponent rules to derive the identities.

2. Usually cos carries a positive sign while sine carries a negative sign.

3. One cannot escape from learning the formulae of reciprocal functions, periodicity of functions and Pythagorean identities.

4. Instead of attempting to cram the identities, try to establish relations between terms so as to minimize the chances of forgetting the formulae.

5. Learn one of the sum identities and the remaining sum identities can be easily derived using the facts that cos x is an even function and sin x is an odd function.

6. It is crucial to have your basics clear as they can help you in reaching the formulae in case you forget or get confused.

7. Always remember that all the trigonometric functions are periodic i.e. they repeat after a specific interval. This concept also proves useful.

8. Once you remember the sum and difference identities for sine and cos i.e. the formulae of sin (a ± b) and cos (a ± b), the multiple angle formulae can be derived from these identities by putting b = a, we get the formula for cos 2a.

9. Practicing numerous questions based on application of these formulae can help you in mugging them up without putting in extra effort.

We have listed all the important trigonometric identities here so that students don’t miss out any:

· Pythagorean Identities

sin ²X + cos ²X = 1

1 + tan ²X = sec ²X

1 + cot ²X = csc ²X

·  Negative Angle Identities

sin (-X) = – sin X, odd function

csc (-X) = – csc X, odd function

cos (-X) = cos X, even function

sec (-X) = sec X, even function

tan (-X) = – tan X, odd function

cot (-X) = – cot X, odd function

· Cofunctions Identities

sin (Ï€ /2 – X) = cos X

cos (Ï€ /2 – X) = sin X

tan (Ï€ /2 – X) = cot X

cot (Ï€/2 – X) = tan X

sec (Ï€ /2 – X) = csc X

csc (Ï€ /2 – X) = sec X

· Addition Formulas

cos (X + Y) = cos X cos Y – sin X sin Y

cos (X – Y) = cos X cos Y + sin X sin Y

sin (X + Y) = sin X cos Y + cos X sin Y

sin (X – Y) = sin X cosY – cos X sin Y

tan (X + Y) = [ tan X + tan Y ] / [ 1 – tan X tan Y]

tan (X – Y) = [ tan X – tan Y ] / [ 1 + tan X tan Y]

cot (X + Y) = [ cot X cot Y – 1 ] / [ cot X + cot Y]

cot (X – Y) = [ cot X cot Y + 1 ] / [ cot Y – cot X]

· Sum to Product Formulas

cos X + cos Y = 2cos[(X + Y)/ 2] cos[(X – Y)/ 2]

sin X + sin Y = 2sin[(X + Y)/ 2] cos[(X – Y)/ 2]

· Difference to Product Formulas

cos X – cos Y = – 2sin[(X + Y) / 2] sin[(X – Y) / 2]

sin X – sin Y = 2cos[(X + Y) / 2] sin[(X – Y) / 2]

· Product to Sum/Difference Formulas

cos X cos Y = (1/2) [cos (X – Y) + cos (X + Y)]

sin X cos Y = (1/2) [sin (X + Y) + sin (X – Y)]

cos X sin Y = (1/2) [sin (X + Y) – sin[ (X – Y)]

sin X sin Y = (1/2) [cos (X – Y) – cos (X + Y)]

· Difference of Squares Formulas

sin ²X – sin ²Y = sin (X + Y) sin (X – Y)

cos ²X – cos ²Y = – sin (X + Y) sin (X – Y)

cos ²X – sin ²Y = cos (X + Y) cos (X – Y)

· Double Angle Formulas

sin (2X) = 2 sin X cos X

cos (2X) = 1 – 2sin ²X = 2cos ²X – 1

tan (2X) = 2tan X/[1 – tan ²X]

·  Multiple Angle Formulas

sin (3X) = 3sin X – 4sin ³X

cos (3X) = 4cos ³X – 3cos X

sin (4X) = 4sin X cos X – 8sin ³X cos X

cos (4X) = 8cos ⁴X – 8cos ²X + 1

· Half Angle Formulas

sin (X/2) = ±√[(1 – cos X)/2]

cos (X/2) = ±√[(1 + cos X)/2]

tan (X/2) = ±√[(1 – cos X)/(1 + cos X)]

= sin X/(1 + cos X)

= (1 – cos X)/sin X

· Power Reducing Formulas

sin ²X = 1/2 – (1/2) cos (2X))

cos ²X = 1/2 + (1/2) cos (2X))

sin ³X = (3/4) sin X – (1/4) sin (3X)

cos ³X = (3/4) cos X + (1/4) cos (3X)

sin ⁴X = (3/8) – (1/2)cos (2X) + (1/8)cos (4X)

cos ⁴X = (3/8) + (1/2)cos (2X) + (1/8)cos (4X)

sin ⁵X = (5/8)sin X – (5/16)sin (3X) + (1/16)sin (5X)

cos ⁵X = (5/8)cos X + (5/16)cos (3X) + (1/16)cos (5X)

sin ⁶X = 5/16 – (15/32)cos (2X) + (6/32)cos (4X) – (1/32)cos (6X)

cos ⁶X = 5/16 + (15/32)cos (2X) + (6/32)cos (4X) + (1/32)cos (6X)

· Trigonometric Functions Periodicity

sin (X + 2Ï€) = sin X, period 2Ï€

cos (X + 2Ï€) = cos X, period 2Ï€

sec (X + 2Ï€) = sec X, period 2Ï€

csc (X + 2Ï€) = csc X, period 2Ï€

tan (X + π) = tan X, period π

cot (X + π) = cot X, period π

The Back Bencher’s Tip to learn the Periodic Table

Trigonometry Study Material