0

Guest

Courses New

Question 3...............................................

Question 3............................................... 

Question Image
Grade:

1 Answers

Samyak Jain
333 Points
5 years ago
Energy stored in a capacitor of capacitance C with potential differnce V across it is (1/2)CV2.
Let C1 and C2 be the capacitances. V = 600 V.
Equivalent capacitance when they are in parallel is C1 + C2. So, energy stored in this combination is
(1/2)(C1 + C2)V2 = 18 J   \Rightarrow  (1/2)(C1 + C2)(6000 V)2 = 18 J
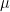
Solving, we get C1 + C2 = 10 – 6 F = 1 \muF
Equivalent capacitance of C1 and C2 when they are in series is C1C2 / (C1 + C2).
So, energy stored is (1/2){C1C2 / (C1 + C2)}V2 = 4 J
(1/2){C1C2 / (C1 + C2)}(6000 V)2 = 4 J,    here put C1 + C2 = 10– 6 F.
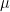
Solving we get C1C2 = (2/9) x 10 – 12 F2  =  (2/9) (\muF)2 .
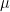
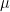
Thus, we have C1 + C2 = 1 \muF  and  C1C2 = (2/9) (\muF)2
i.e. we want factors of 2/9 whose sum is 1. Such factors are 1/3 and 2/3.
\therefore C1 = 1/3 \muF  and  C2 = 2/3 \muF.

Think You Can Provide A Better Answer ?

Other Related Questions on Electrostatics

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More