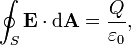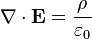Dear Abhijeet,

In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution ofelectric charge to the resulting electric field. Gauss's law states that:

The electric flux through any closed surface is proportional to the enclosed electric charge.^[1]

The law was formulated by Carl Friedrich Gauss in 1835, but was not published until 1867.^[2] It is one of four of Maxwell's equations which form the basis of classical electrodynamics, the other three being Gauss's law for magnetism, Faraday's law of induction, and Ampère's law with Maxwell's correction. Gauss's law can be used to derive Coulomb's law,^[3] and vice versa.

Gauss's law may be expressed in its integral form:

where the left-hand side of the equation is a surface integral denoting the electric flux through a closed surface S, and the right-hand side of the equation is the total charge enclosed by S divided by the electric constant.

Gauss's law also has a differential form:

where ∇ · E is the divergence of the electric field, and ρ is the charge density.

The integral and differential forms are related by the divergence theorem, also called Gauss's theorem. Each of these forms can also be expressed two ways: In terms of a relation between the electric field E and the total electric charge, or in terms of the electric displacement field D and thefree electric charge.

Gauss's law has a close mathematical similarity with a number of laws in other areas of physics, such as Gauss's law for magnetism andGauss's law for gravity. In fact, any "inverse-square law" can be formulated in a way similar to Gauss's law: For example, Gauss's law itself is essentially equivalent to the inverse-square Coulomb's law, and Gauss's law for gravity is essentially equivalent to the inverse-squareNewton's law of gravity.

Deriving Coulomb's law from Gauss's law

Strictly speaking, Coulomb's law cannot be derived from Gauss's law alone, since Gauss's law does not give any information regarding thecurl of E (see Helmholtz decomposition and Faraday's law). However, Coulomb's law can be proven from Gauss's law if it is assumed, in addition, that the electric field from a point charge is spherically-symmetric (this assumption, like Coulomb's law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).

Taking S in the integral form of Gauss's law to be a spherical surface of radius r, centered at the point charge Q, we have

By the assumption of spherical symmetry, the integrand is a constant which can be taken out of the integral. The result is

where  is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we get

which is essentially equivalent to Coulomb's law. Thus the inverse-square law dependence of the electric field in Coulomb's law follows from Gauss's law.

              Good Luck!!!!!!!

    Plz. approve it by clicking 'Yes' given below!!!!!!1   Plz. Plz. Plz.!!!!!!!!!

gauss's law....

                      it states that electric flux coming out of a closed surface will be

1/epsilon not times the charge on closed srface.

i.e.  

?=1/epsilon not (q)

In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution ofelectric charge to the resulting electric field. Gauss's law states that:

The electric flux through any closed surface is proportional to the enclosed electric charge.^[1]

The law was formulated by Carl Friedrich Gauss in 1835, but was not published until 1867.^[2] It is one of four of Maxwell's equations which form the basis of classical electrodynamics, the other three being Gauss's law for magnetism, Faraday's law of induction, and Ampère's law with Maxwell's correction. Gauss's law can be used to derive Coulomb's law,^[3] and vice versa.

Gauss's law may be expressed in its integral form:

where the left-hand side of the equation is a surface integral denoting the electric flux through a closed surface S, and the right-hand side of the equation is the total charge enclosed by S divided by the electric constant.

Gauss's law also has a differential form:

where ∇ · E is the divergence of the electric field, and ρ is the charge density.

The integral and differential forms are related by the divergence theorem, also called Gauss's theorem. Each of these forms can also be expressed two ways: In terms of a relation between the electric field E and the total electric charge, or in terms of the electric displacement field D and thefree electric charge.

Gauss's law has a close mathematical similarity with a number of laws in other areas of physics, such as Gauss's law for magnetism andGauss's law for gravity. In fact, any "inverse-square law" can be formulated in a way similar to Gauss's law: For example, Gauss's law itself is essentially equivalent to the inverse-square Coulomb's law, and Gauss's law for gravity is essentially equivalent to the inverse-squareNewton's law of gravity.

Gauss's law can be used to demonstrate that all electric fields inside a Faraday cage have an electric charge. Gauss's law is something of an electrical analogue of Ampère's law, which deals with magnetism.