Vectors

 

Table of Content

Unit Vectors Base Vectors and Vector Components Negative of a Vector Some Key Points Some Basic Rules of Vectors

Vectors constitute an important topic in the Mathematics syllabus of JEE. It is important to master this topic to remain competitive in the IIT JEE. It often fetches some direct questions too. The topic of Vectors is quite simple and it also forms the basis of several other topics.

Various topics that have been covered in this chapter include:

• Introduction

• Addition of Two Vectors

• Fundamental Theorem of Vectors

• Orthogonal System of Vectors

We now discuss some of these topics in brief as they have been covered in detail in the coming sections:

Length / Magnitude of a vector: The length or magnitude of the vector w = (a, b, c) is defined as

|w|= w= √a²+b²+c²

Unit Vectors

A unit vector is a vector of unit length. A unit vector is sometimes denoted by replacing the arrow on a vector with a "^" or just adding a "^" on a boldfaced character (i.e., ? or ?). Therefore,

 | ?| = 1.

Any vector can be made into a unit vector by dividing it by its length.

? = u / |u|

Any vector can be fully represented by providing its magnitude and a unit vector along its direction. A vector can be written as u = u?

You may refer the Sample Papers to get an idea about the types of questions asked.
 

Base Vectors and Vector Components

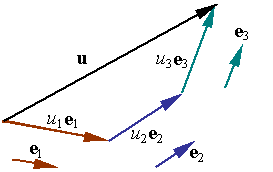
Base vectors represent those vectors which are selected as a base to represent all other vectors. For example the vector in the figure can be written as the sum of the three vectors u₁, u₂, and u₃, each along the direction of one of the base vectors e₁, e₂, and e₃, so that 

u= u₁+u₂+u₃

It is clear from the figure that each of the vectors u₁, u₂ and u₃ is parallel to one of the base vectors and can be written as a scalar multiple of that base. Let u₁, u₂, and u₃ denote these scalar multipliers such that one has

u₁= u₁e₁

u₂=u₂e₂

u₃=u₃e₃

The original vector u can now be written as

u= u₁e₁+u₂e₂+u₃e₃
 

Watch this Video for more reference
 

 

Negative of a Vector

A negative vector is a vector that has the opposite direction to the reference positive direction.

A vector connecting two points:

The vector connecting point A to point B is given by

r= (x_B-x_A) i+ (y_B – y_A) j + (z_B – z_A)k , here i, j and k denote the unit vectors along x, y and z axis respectively.
 

Some Key Points

• The magnitude of a vector is a scalar and scalars are denoted by normal letters.

• Vertical bars surrounding a boldface letter denote the magnitude of a vector.  Since the magnitude is a scalar, it can also be denoted by a normal letter;
  |w| = w denotes the magnitude of a vector

• The vectors are denoted by either drawing a arrow above the letters or by boldfaced letters.

• Vectors can be multiplied by a scalar. The result is another vector.

Suppose c is a scalar and v = (a, b) is a vector, then the scalar multiplication is defined by cv= c (a,b)= (ca,cb). Hence each component of a vector is multiplied by the scalar.

• If two vectors are of the same dimension then they can be added or subtracted from each other. The result is gain a vector. dd

Then the sum of these two vectors is defined by

v + u = (a + e, b + f, c + g).

• We can also subtract two vectors of the same direction. The result is again a vector. As in the previous case subtracting vector u from v yields v - u = (a - e, b - f, c - g). the difference of these vectors is actually the vector

v - u = v + (-1)u.
 

Some Basic Rules of Vectors

If u, v and w are three vectors and c, d are scalars then the following hold true:

• u + v = v + u (the commutative law of addition)

• u + 0 = u

• u + (-u) = 0 (existence of additive inverses)

• c (du) = (cd)u

• (c + d)u = cu +d u

• c(u + v) = cu + cv

• 1u = u

• u + (v + w) = (u + v) + w (the associative law of addition)

To read more, Buy study materials of Vectors comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.