System of Trigonometric Equations | IIT JEE Math Trigonometry

In the earlier sections we have already learnt how to solve trigonometric equations in one variable. But you must have seen various questions in the past year papers involving more than one variable. There are some standard patterns of questions on trigonometric equations with more than one variable which are always asked in most of the competitive exams.

Once you are comfortable and have a solid foundation of trigonometric equations with one variable, this topic won’t be very difficult for you. Though there is no established way of dealing with all the problems but once you go through various possible ways, you will surely be able to handle the IIT JEE problems.

Kindly go through the below listed tricks and the standard steps of dealing with such problems. Most of the problems can be tackled by these tips:

(1) If possible, reduce the equation in terms of any one variable, preferably x. Then solve the equation as you used to in case of a single variable.

(2) Try to derive the linear/algebraic simultaneous equations from the given trigonometric equations and solve them as algebraic simultaneous equations.

(3) At times, you might be required to make certain substitutions. It would be beneficial when the system has only two trigonometric functions.  

Illustration: Solve for general x, y,

sin (x – y) = 2 sin x sin y, where x and y are two acute angles of right angled triangle.

Solution: Since it is given that x and y are two acute angles of right triangle, so we make the substitution y = π/2 – x in first equation and transform it as follows:-

sin (2x - π/2) = 2 sin x sin (π/2 - x)

⇒ – sin (π/2 - 2x) = 2sin x cos x

⇒ –cos 2x = sin 2x

⇒ tan 2x = –1 = tan (-π/4)

⇒ 2x = n π – π/4, where n = 0, ±1, ±2, ………

or, x = nπ/2 - π/8, where n = 0, ±1, ±2, ………

y = nπ/2 - 5π/8, where n = 0, ±1, ±2, ………

Hence solution is {nπ/2 + π/8, 5π/8 - πn/2}.

Illustration: Given that sin x (cos y + 2sin y) – cos x (2cos y - sin y) = 0, find the value of tan (x + y).

Solution: sin x (cos y + 2sin y) – cos x (2cos y - sin y) = 0

Remove the parentheses:

sin x*cos y + 2sin x*sin y - 2cos x*cos y + cos x*sin y = 0

Rearrange the terms:

sin x*cos y + cos x*sin y - 2cos x*cos y + 2sin x*sin y = 0

Factor -2 out of the 3rd and 4th terms:

sin x*cos y + cos x*sin y - 2(cos x*cos y – sin x*sin y) = 0

Use the identity sin (A + B) = sin A*cos B + cos A*sin B to rewrite the first two terms:

sin (x + y) - 2(cos x*cos y – sin x*sin y) = 0

Use the identity cos(A + B) = cos A*cos B - sinA*sin B to rewrite the two terms inside the parentheses. Hence, the equation gets reduced to  
sin (x + y) - 2*cos(x + y) = 0

Divide throughout by cos(x + y)

{sin (x + y)}/ {cos (x + y)} – {2*cos (x + y)} / {cos (x+y)} = 0

Using the identity tan A = sin A/ cos A to rewrite the beginning terms and after simplification, we obtain

tan (x + y) - 2 = 0

which gives tan (x + y) = 2.

Watch this Video for more reference

Illustration: Solve the system of equations 

sin² x + sin² y = 1/2.

x – y = 4π/3 

Solution: We transform the first equation of the system– 

1/2 (1 – cos 2x) + 1/2 (1 – cos 2y) = ½

cos 2x + cos 2y = 1 &

2 cos (x + y).cos(x – y) = 1

Hence it is clear that the system– 

cos (x + y) cos (x – y) = 1/2     …… (1)

x – y = 4π/3                                …… (2)

has the same solution as the original system, i.e. the systems are equivalent.

So, from equation (1) and (2) we have

cos (x + y) cos (4π/3) = 1/2 or cos (x + y) = –1

x + y = 2nπ ± π

Hence we have two linear equations in x and y

x + y = 2n π ± π, n ∈ I

x – y = 4π/3

x = nπ + 2π/3 ± π/2      …… (a) 

Taking +ve sign of (a)

x = (n +7/6)π 

   = kπ, k = (n +7/6) and y = kπ – 4π/3

Taking –ve sign of (a)

x = nπ + π/6

y = nπ + π/6-4π/3

   = n π – 7π/6.

The general solution of system of equations is given by (kπ, kπ - 4π/3) and (nπ + π/6, nπ -7π/2) where k = n + 7/6, n ∈ I 

So, these are the solutions to the original system.

Note: In the previous examples we have written the relationships between the unknowns x and the set of solution of the system has been expressed in terms of only one integral parameter e.g. n, k etc. But in practical applications, we may sometimes require to express the general solution in terms of two integral parameters while solving a system of equations with two variables. 

Often, you will find that introducing a new variable helps an equation efficiently. Introduction of New Variables can be employed in those cases where a system contains only two trigonometric functions or can be reduced to such a form. Let us see an illustration. 

Illustration: Solve the system 

sin x + cos y = 1          ……… (1) 
cos 2x – cos 2y = 1      ……… (2) 
Solution: We can transform the equation (2) by putting cos 2x = 1 – 2sin² x and cos 2y = 2 cos² y –1 
cos 2x – cos 2y = 1 – 2 sin² x + 1 – 2 cos² y = 1 
⇒ sin² x + cos² y = 1/2 
and hence our system is 
sin x + cos y = 1          ……… (3) 
sin² x + cos² y = 1/2     ……… (4) 
which is equivalent to the original system. 
For simplicity, let us put sin x = y, cos y = v [note → u ∈ [–1, 1] and v ∈ [–1, 1] and hence 
u + v = 1          ………… (5) 
u² + v² = 1/2     ………… (6)

solving (5) and (6) we get,

u = sin x = 1/2 

v = cos y = ½

Hence, the general solution of the given system of equations is given by 

x = mπ + (–1)m π/6, m ∈ I 

y = 2nπ + π/3, n ∈ I 

The solution of various pairs formed from these values of x and y is precisely the set of all solution of the original system.

Remark: How can we solve the equation when the terms on the two sides (LHS and RHS) of the equation are of different nature e.g.  trigonometric and algebraic? 

This type of problem can be solved by using inequality method. This method is used for testing whether the equation has any real solution or not, following steps are advised to be followed. 

Step I: Let y = each side of the equation i.e. break the equation in two parts. 

Step II: Find the inequality for y taking LHS of the equation and also for RHS of the equation. If there is any value of y satisfying both the inequalities, then there will be a real solution and otherwise there will be no real solution. 

Illustration: Show that the equation 

2 cos² (x/2) sin² x = x² + x^-2 for 0 < x ≤ π/2 has no real solution.

Solution: This is a problem where LHS is in trigonometric form and RHS is in algebraic form. So we will use inequality method. 

Let y = 2 cos² (x/2) sin² x         ……… (1) 

and y = x² + x^-2 ……… (2) 

from (1), y = 2 cos² x/2 sin² x

= (1 + cos x) sin² x

= (a number < 2) × (a number < 1) 

< 2 [? for 0 < x < π/2, 0 < cos x < 1 and 0 < sin x < 1] 

i.e. y < 2            ……… (3)

from (2), y = x² + x^-2

A.M. > G.M.

(x² + x^-2)/2 ≥ √(x².x^-2 )

x² + x² > 2

i.e. y > 2           ……… (4) 

No value of y can be obtained satisfying (3) and (4) simultaneously, since y cannot be greater as well as less than 2 simultaneously.

⇒ no real solution of the equation exists. 

Note: Some problems can be solved using graphs. The number of intersection point is equal to number of solution. 

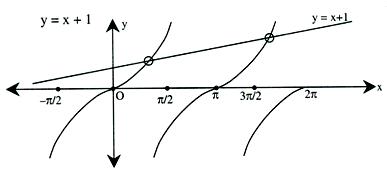
Illustration: Find the number of roots of the equation tan x = x + 1 between –π/2 and 2 π. 

Solution: Again, this is a problem of trigonometric form on LHS and algebraic form on RHS. 

This can be solved by plotting the graph 

Let y = tan x

y = x + 1 

The number of intersecting points is two which means that the number of solutions is 2.
Note: In both illustrations we have used two different ways to solve. We opt for graphical method if tracing is easier otherwise we opt for inequality method.
 

Summary of Important Points 

Since trigonometric functions are periodic functions, solutions of trigonometric equations can be generalized with the help of the periodicity of the trigonometric functions. The solution consisting of all possible solutions of a trigonometric equation is called its general solution. 

We use the following formulae for solving the trigonometric equations: 

• sin θ = sinα and cosθ = cosα ⇒ θ = 2nπ + α 

• sinθ = 0 ⇒ θ = nπ 

• cosθ = 0 ⇒ θ = (2n + 1)π/2 

• tanθ = 0 ⇒ θ = nπ 

• sinθ = sinα ⇒ θ = nπ + (–1)nα,where α ∈ [–π/2, π/2] 

• cosθ = cosα ⇒ θ = 2nπ ± α, where α ∈ [0, π] 

• tanθ = tanα ⇒ θ = nπ + α, where α ∈ (–π/2, π/2)

• sin2θ = sin2α, cos2θ = cos2α, tan2θ = tan2α ⇒ θ = nπ ± α 

• sinθ = 1 ⇒ θ = (4n + 1)π/2 

• sinθ = –1 ⇒ θ = (4n – 1)π/2 

• sinθ = –1 ⇒ θ = (2n + 1)π/2 

• |sinθ| = 1 ⇒ θ = 2nπ

• cosθ = 1 ⇒ θ = (2n + 1)π

• |cosθ| = 1 ⇒ θ = nπ 

Note: Everywhere in this chapter n is taken as an integer, if not stated otherwise. 

The general solution should be given unless the solution is required in a specified interval or range.

α is taken as the principal value of the angle. Numerically least angle is called the principal value. 

Remarks: 

While solving a trigonometric equation, squaring the equation at any step should be avoided as far as possible and if unavoidable, check the solution for extraneous values.

Never cancel terms containing unknown terms on the two sides, which are in product. It may cause loss of genuine solution.

Sometimes the solution of equation may result into more than one solution sets. These solution sets may be disjoint, overlapping or superimposed. If the solution sets are overlapping, we try to rewrite the solution in such a way that the common solutions are included in one of the solution sets only. If one of the solution set comes out to be the subset of other than we omit the subset form the final solution set.

Illustration: The number of solutions of the pair of equations 2 sin2θ – cos 2θ = 0 and 2cos2θ – 3 sin θ = 0 in the interval [0, 2π] is

(a) 0

(b) 1

(c) 2

(d) 4

Solution: Considering the first equation 2 sin2θ – cos 2θ = 0

This gives sin2θ = ¼

Also, the second equation is 2cos2θ – 3 sin θ = 0

Hence, this means 2cos2θ = 3 sin θ.

which gives sin θ = 1/2.

Hence, the two solutions exist in the interval [0, 2π].
 

Related Resources

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

• Fast Track your revision with the ultimate Revision Notes on Trigonometry.

To read more, Buy study materials of Trigonometry comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.