Theoretical Explanation of Continuous Spectrum

Production of Continuous Spectrum

When light is passed through a prism or a diffraction grating to produce a spectrum, the type of spectrum you will see depends on what kind of object is producing the light. Many hot objects emit a continuous spectrum of radiation, containing light of all wavelengths. A hot gas may instead produce an emission spectrum, consisting only of a few well-defined emission lines of specific frequencies, or colors. Passing a continuous beam of radiation through cool gas will produce absorption lines at precisely the same frequencies as are present in the gas's emission spectrum. There are two basic types of spectra: continuous spectrum (energy at all wavelengths) and discrete spectrum (energy at only certain wavelengths). Astronomers usually refer to the two types of discrete spectra: emission lines (bright lines) and absorption lines (dark lines in an otherwise continuous spectrum) as different types of spectra.

A rainbow is an example of a continuous spectrum. Most continuous spectra are from hot, dense objects like stars, planets, or moons. The continuous spectrum from these kinds of objects is also called a thermal spectrum, because hot, dense objects will emit electromagnetic radiation at all wavelengths or colors. Any solid, liquid and dense (thick) gas at a temperature above absolute zero will produce a thermal spectrum. A thermal spectrum is the simplest type of spectrum because its shape depends on only the temperature. A discrete spectrum is more complex because it depends on temperature and other things like the chemical composition of the object, the gas density, surface gravity, speed, etc. Exotic objects like neutron stars and black holes can produce another type of continuous spectrum called synchrotron spectrum from charged particles swirling around magnetic fields, but I will discuss them in another chapter later on. For now, let's look at a thermal spectrum.

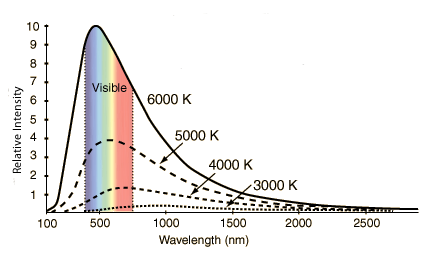
Black Body Radiation

Sometimes astronomers use the term blackbody spectrum for a thermal spectrum. A blackbody is an object that absorbs all the light falling on it, reflecting none of it, hence, it appears black. When the blackbody object is heated, it emits light very efficiently without any gaps or breaks in the brightness. Though no object is a perfect blackbody, most stars, planets, moons and asteroids are near enough to being blackbody, that they will produce spectra very similar to a perfect thermal spectrum. The below figure showes the spectral curve for black body radiation.

The accelerated electrons are suddenly stopped by the target. According to Maxwell's theory, wherever a charged particle is accelerated or decelerated, they emit radiation. This is called Bremsstrahlung or braking radiation. 

When the whole of the energy of the electron is converted to radiation, one gets the maximum energy or λ minimum.

If V is the potential difference applied, it is converted to the kinetic energy of the electron. If Ve = E = h, then the wave-length λ = hc/E.

If hc = 12400 eVÅ, and if E is given in eV, then, λ_min = hc/E which will be in Å.

When the electrons lose their energy by multiple collisions and penetration inside the target, the radiation, produced has less energy.The energy that is not converted to radiation only heats up the target. It has to be cooled property to prevent damage to the X-ray tube. The maximum value of intensity is approximately at 3/2λ_min (This is often marked λminActually it is not the maximum value of λ but λ at intensity maximum).The distribution of intensity depends on the material of the target, the current and the potential difference applied. 

I α V² and I (intensity) α (current)

The current is normally in milli-amperes and the voltage in kilovolts.

Refer this video to know more about continuous spectrum:-

Problem 1 :-

If the wavelength of the Kα line of platinum is 0.2Å, what is the energy needed to excite this line? (the energy of the first level of platinum, |E_n–1| = 81keV). What is the corresponding absorption energy? What is the ionization energy of platinum?

Solution:-

The energy corresponding to Q.2Å is ΔE = 12400eV – A / 0.2 A = 62 × 10³ eV = 62 KeV

But if one gives 62 keV energy to the electron in the x-ray tube, one cannot at Kαx-ray line because the higher levels are full. K_α line can be excited only when a vacancy is created in the ground state, i.e to remove the electron from the k-level. The energy required is obviously the ionization energy of the k-level. which is 81 keV. There is no absorption line corresponding to theK_α emission line. In x-rays one gets only absorption edge (see the theory part).

The ionization energy of the k-level is same as the k-absorption edge which is the energy of excitation of the k-electron. This is 81 keV for platinum.

______________________________________________________________________________________________

Problem 2 :-

An X-ray tube, operated at a potential difference of 40 kV, produces heat at the rate of 720 W. Assuming 0.5% of the energy of the incident electrons is converted into X-rays. Calculate

(i) The number of electrons per second striking the target.

(ii) The velocity of the incident electrons.

Solution:-

(i) Heat produced per second at the target is

P = 0.995 VI (0.5% of energy is converted into X-rays)

So, I = P/0.995 V = 720/(0.995)(40×10³) = 0.018 A

The number of electrons per second incident on the target

n = 1/e = 0.018 / 1.6 × 10^–19 = 1.1 × 10¹⁷ electrons 

(ii) Energy of incident electrons 1/2 mv² = eV

or  v √2eV / m = 1.2 × 10⁸ m/s

Question 1 :-

?The radiations emitted form hydrogen filled discharge tube show

(a)band spectrum              (b) line spectrum

(c)continuous spectrum     (d)absorption spectrum

Question 2 :-

Which one of following postulate is in accordance with the Rutherfords model?

(a) continuous spectra for atoms              (b) discrete spectra for atoms

(c) either continuous nor discrete             (d) no spectrum

Question 3 :-

Wave-like characteristic of electron is demonstrated by

(a) Line spectrum of atoms.                  (b) Production of x-rays.

(c) Diffraction by crystalline solids.        (d) Photoelectric effect.

Question 4 :- 

Radiation with wavelength longer than red lights

(a) ultraviolet rays                       (b) X-rays

(c) infrared radiation                    (d) visible radiation

Related Resources

• You might like to refer Emission of Electrons.

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

• To get answer to any question related to continuous spectrum click here.

To know more about continuous spectrum, please fill up the form given below:-