Algebraic Operations on Differentiation and Important Formulae

Algebraic Operations

As discussed in the previous sections, differentiation is a simple concept and we have already discussed the calculation of various functions like implicit and composite functions. In this section, we shall throw some light on algebraic operations in differentiation. Henceforth, we shall switch to the important differentiation formulae.

Yes it is possible to define algebraic operations in differentiation.

If u = f(x) and v = g(x) are differentiable functions then

(a) d/dx [f(x) + g(x)] = (d/dx) f(x) + (d/dx) g(x)

By first principle method

L.H.S. (d/dx) [f(x) + g(x)] = lim _h→0 (f(x+h) + g(x+h) – g(x) – f(x))/h

= lim _h→0 (f(x+h) – f(x))/h + lim _h→0 (g(x+h) - g(x))/h

= (d/dx) f(x) + (d/dx) g(x)

= R.H.S.

(b) (d/dx) [f(x) – g(x)] = (d/dx) f(x) - (d/dx) g(x)

(c) Product Rule of Differentiation:

(d/dx) [f(x).g(x)] = f(x) (d/dx) g(x) + g(x) (d/dx) f(x)

In order to derive this result, proceed as follows:

Let h(x) = f(x) g(x)

⇒ h'(x) = lim _h→0 (h(x + h) - h(x))/h

= lim _h→0 (f(x+h) g(x+h) – f(x) g(x))/h

=  lim _h→0 (f(x+h) g(x+h) – f(x+h) g(x) + f(x+h) g(x) – f(x) g(x))/h

= lim _h→0 f(x+h) [g(x+h) – g(h)]/h + g(x) lim _h→0 [f(x+h) – f(x)]/h

= f(x) (d/dx) g(x) + g(x) (d/dx) f(x)

= f(x) g'(x) + g(x) f'(x)

= R.H.S.

Result:

Suppose you have three functions say j(x), k(x) and l(x). Then

Note: 

This method can be generalized for product of differentiable functions as follows:

Suppose we have n functions f₁, f₂ , ….... , f_n.

Then the derivative of the product of these n functions is given by 

d/dx (f₁.f₂.f₃. ..............  .f_n) = f'₁ f₂ f₃ ........ f_n + f₁ f'₂ f₃...... f_n + f₁ f₂f'₃ ........ f_n + ....... + f₁ f₂ f₃ ....... f'_n

(d) Quotient Rule of Differentiation:

If we have a function of the form y = (g(x)/h(x)), then the derivative is given by 

D(g(x)/h(x)) = [h(x)g’(x) – g(x).h’(x)]/ h²(x)

In fact, this formula can be remembered as 

Remark: 

In particular, if you have a function of the form y = 1/f(x), then D(y) = – f’(x)/f²(x).

Illustration 3:

Find the differentiation coefficient of e^x/log x with respect to x.

Solution:

The given function is y = e^x/log x

dy/dx = log x . d/dx  e^x - e^x d/dx (log x)/(log x)²

= (log xe^x - e^x/x)/(log x)²

= (x log xe^x - e^x)/ x(log x)² = (e^x (x log x – 1))/(x (log x)²)

If y = f(u) and u = g(x), then dy/dx = dy/dx. du/dx = f'g(x) g'(x)

e.g. Let y = [f(x)]ⁿ. We put u = f(x). So that y = uⁿ.

Therefore, using chain rule, we get

dy/dx = dy/dx.du/dx = nu^(n-1) [f'(x)]^(n-1) f' (x)

Having discussed various differentiation rules including product differentiation and related examples, we now switch to important formulas for differentiation:
 

Important Differential Formulae

First of all we begin with the differentiation of Algebraic, Exponential, Logarithmic and antilogarithmic functions and then we shall move to the trigonometric functions:

1.  d/dx (xn) = nxn-1                      

2.  d(ex)/dx = ex

3.  d/dx (loge x) = 1/x ∀ x > 0

4. d/dx (xn) = nxn-1       

5. d/dx (loga x) = 1/x logae ∀ x > 0

Differentiation of trigonometric functions

 1. d/dx (sin x) = cos x

 2. d/dx (cos x) = - sin x

 3. d/dx (tan x) = sec2x

 4. d/dx (cot x) = - cosec2x

 5. d/dx (sec x) = sec x tan x

 6. d/dx (cosec x) = - cosec x cot x

Differentiation of Inverse circular function

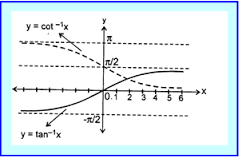 1. d/dx (sin-1x) = 1/√(1 – x2); |x| < 1

 2. d/dx (cos-1x) = (-1)/√(1 – x2)

 3. d/dx (tan-1x) = 1/(1 + x2); x ∈ R

 4. d/dx (cot-1x) = 1/(1 + x2) ; x ∈ R

 5. d/dx (sec-1x) = 1/(|x|√(x2-1)); x > 1

 6. d/dx (cosec-1x) = (-1) / (|x| √ (x2-1)); x > 1

General Theorems on Differentiation

1. d/dx (c) = 0

2. d/dx [a f(x) + b g(x)] = af'(x) + b g'(x)

3. d/dx [f(x)g(x)] = f' (x)g(x) + f(x) g'(x)

4. d/dx [f(x)/g(x)] = (g(x) f'(x) - f(x) g'(x))/[g(x) ]2

5. d/dx [f(x)g(x) ] = f(x)g(x) [g(x)/f(x) f'(x) + g' (x) ln f(x)]

Q1. (d/dx) [f(x).g(x)] = 

(a) f(x) (d/dx) g(x) + g(x) (d/dx) f(x)

(b) f(x) (d/dx) g(x) + g(x) (d/dx) f(x)

(c) f(x) (d/dx) g(x) + g(x) (d/dx) f(x)

(d) f(x) (d/dx) g(x) + g(x) (d/dx) f(x)

Q2. Quotient rule of differentiation gives 

(a) D[g(x)/h(x)] = [h(x)g’’(x) – g(x).h’(x)]/ h²(x)

(b) D[g(x)/h(x)] = [h’(x)g(x) – g’(x).h’(x)]/ h²(x)

(c) D[g(x)/h(x)] = [h(x)g’(x) – g(x).h’(x)]/ h(x)

(d) D[g(x)/h(x)] = [h(x)g’(x) – g(x).h’(x)]/ h²(x)

Q3. In case of differentiation of three functions f(x), g(x) and h(x), 

(a) D(f(x)g(x)h(x)) = [(fg)’(h) + (gh)’(f) + (hf)’(g)]/2

(b) D(f(x)g(x)h(x)) = [(fg)’(h) + (gh)’(f) + (hf)’(g)]

(c) D(f(x)g(x)h(x)) = [(fg)(h)’ + (gh)’(f) + (hf)’(g)]/2

(d) none of the above

Q4. The derivative of the difference of two functions is

(a) The difference of product of the functions and their derivatives

(b) first function derivative of second minus second function mulitp[lied by the derivative of first.

(c) the difference of derivatives of the individual functions.

(d) can’t say

Q5. d/dx (loga x) = 

(a) 1/x log_e a   ∀ x > 0

(b) 1/x logae ∀ x > 0

(c) 1/x logae 

(d) 1/x² logae ∀ x > 0

Related Resources

• You may wish to refer General Theorems of Differentiation.

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Methods of Differentiation comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.