Differentiation

 

Table of Content

Derivatives Differentiation  Notation Geometrical Interpretation of Differentiation Rules of differentiation Logarithmic Differentiation Steps of Logarithm Differentiation Related Resources

Derivatives

Derivative is the rate of change in the slope of the curve of the function.

Derivative can be finding using the formula,

At some places derivatives are also represented by fꞌ(x).
 

Differentiation

The process of finding a derivative is called Differentiation. Normally a dependent variable is expressed in terms of independent variables by means of an equation. Now when we find the differential coefficient of the dependent variable with respect to the independent variable, what we do is we try to find out another equation by which the change in the dependent variable (for any infinitesimal change in independent variable) is relatable to the independent variable, whatever be the value of the independent variable.

Hence, derivative is a measure of how a function changes as its input changes. Informally, the derivative is the ratio of the infinitesimal change of the output over the infinitesimal change of the input producing that change of output. Geometrically, for a real valued function of a single real variable, the derivative at a point equals the slope of the tangent line to the graph of the function at that point. The process of finding a derivative is called differentiation.

In fact, differentiation and integration are the two fundamental operations in single-variable calculus. The figure given below illustrates the exact difference between integration and differentiation:

Notation

There are a number of ways of writing the derivative of a function. Though all these are same but it is essential to know them so as to avoid any kind of confusion:

Suppose we are finding the derivative of x², then its derivative may be written as:

• If y = x², dy/dx = 2x

• d/dx (x²) = 2x

This says that the derivative of x² with respect to x is 2x.

• If f(x) = x², f'(x) = 2x

This says that is f(x) = x², the derivative of f(x) is 2x.
 

Geometrical Interpretation of Differentiation

Let y = f(x) be a function, and let P(a, f(a)) and Q(a+h, f(a+h)) be two points on the graph of the function that are close to each other. This graph is shown below:

Joining the points P and Q with a straight line gives us the secant on the graph of the function. And in the ?PQR, the gradient of the line is given by

m = {f(a+h) – f(a)}/(a+h-a) = {f(a+h) – f(a)} / h

In limiting process, i.e. as Q approaches P, h becomes really small, almost close to zero.

Hence, m = (change in y)/(change in x) 

= {f(a+h) – f(a)} / h

 lim _h→0 (?y/?x) = {f(a+h) – f(a)} / h

As Q → P, the chord/secant PQ tends to be a tangent at P for the curve y = f(x). Thus the limiting becomes the slope of the tangent at P for y = f(x).

We denote lim _h→0 (?y/?x) = dy/dx, and

lim _h→0 [f(a+h) – f(a)]/ h = f’(a) 

Therefore dy/dx = f’ (a) = m

Now, we have already seen that ‘m’ is the slope or gradient of the tangent at P for f(x).

f’(a)  =  tan θ  = slope of f(x) at x = a.
 

Rules of differentiation

The differentiation of functions is carried out in accordance with some rules. These differentiation rules have been listed with the help of the following chart:

All these rules will be discussed in detail in the coming sections. Here, we shall give a brief outline of these rules:

(1) Constant rule:

If the function f is a constant, then its derivative is zero. Moreover if a function is multiplied by a constant then its derivative is given by 

{cf(x)}' = cf'(X)

(2)  Sum Rule:

{f(x) ± g(x)}' = f'(x) ± g'(x)

(αf + βg)' = αf' + βg' , for all functions f and g and real numbers α and β.

(3) Product Rule:

(fg)' = f'g + g'f, for all functions f and g.

(4) Quotient Rule:

(f/g)' = (f'g – fg')/g², for all functions f and g such that g ≠ 0.

(5) Chain Rule:

If f(x) = h(g(x)), then f'(x) = h'(g(x)). g'(x)

So while using the chain rule remember the following points: (i) Express the original function as a simpler function of u, where u is a function of x. (ii) Differentiate the two functions you now have. Multiply the derivatives together, leaving your answer in terms of the original function (i.e. in x's rather than u's).

Logarithmic Differentiation

To differentiate some special functions using logarithm is called Logarithm Differentiation. When it is difficult to differentiate the function then we use the differentiation using logarithms.
Logarithm Differentiation starts with taking the natural logarithm that is, logarithm to the base e on the both sides. 

In order to compute the derivative of:

• A function which is the product or quotient of a number of functions

y = g₁(x)g₂(x)g₃(x) ….. or [(g₁(x) g₂(x) g₃(x) ….) / (h₁(x) h₂(x) h₃(x) ….)

• A function of the form [f(x)]^g(x) where f and g are both derivable, it is better to take the logarithm of the function first and then differentiate.

• Or, we can write it as y = (f(x))^g(x) = e ^{g(x).ln f(x)?​}

Example

Differentiate y = xx

Solution:

y = xx

We will take the logarithm to both sides

In y = In xx

       = x In x

Now we will differentiate both sides by using chain rule to the left-hand side as y represents a function of x and use the product rule on the right-hand side.

Multiply both sides with y

yꞌ = y (1 + In x)

    = x^x(1 + In x)

?We list below certain differentiation formulae for finding the derivative of functions:

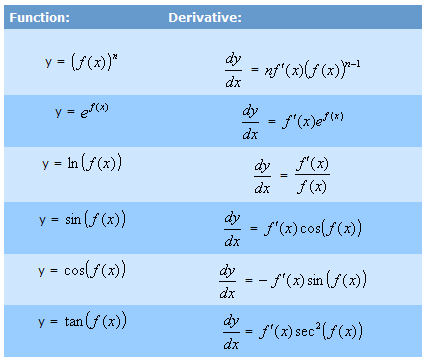
Given below are some more formulae of some logarithmic and trigonometric functions:

d/dx (xx) = xx (1 + ln x) d/dx (logax) = 1/ x ln a d/dx (loga f(x)) = 1/ f(x) ln a . d/dx f(x) d/dx (sin x) = (sin x)' = cos x (cos x)' = -sin x (tan x)' = sec2 x (sec x)' = sec x tan x (cosec x)' = -cosec x cot x (cot x)' = -cosec2x

Steps of Logarithm Differentiation

Logarithm Differentiation is the shortcut which helps in differentiating without using the product rule.

If we have to differentiate the above function then we don’t need to multiply it at all

Step 1: We can take the natural logarithm of both sides.

Step 2: use the product rule of the log.

log_a(m × n) = log_am + log_an

So it will be like this

Step 3: Differentiate both sides using the chain rule of differentiation.

Step 4: Multiply both sides with f(x).

We now discuss some of the differentiation examples followed by some differentiation questions:

Illustration 1:

What is the gradient of the curve y = 2x³ at the point (3, 54)?

Solution:

The gradient of the curve is given by its derivative so the question actually requires you to compute the derivative.

The derivative is dy/dx = 6x²

When x = 3, dy/dx = 6 × 9 = 54.

Hence, the required gradient is 54.

________________________________________________________________________________

Illustration 2:

Find the derivative of  

Solution:

We will use the quotient rule to find the derivative.

Now we know that

 ……….(1)

  …….(2)

Hence, combining (1) and (2) we get the required answer.

_______________________________________________________________________________

Illustration 3:

Find the derivative of f(x) = x⁴ + sin (x²) – ln (x)e^x + 7.

Solution: 

Using the formulae, we get the derivative as

___________________________________________________________________________-

Illustration 4: 

Find the derivative of (x² + 5x – 3)/ 3 x^½.

Solution:

This looks hard, but it isn't. The trick is to simplify the expression first: do the division (divide each term on the numerator by 3x^½.

Doing this we obtain

(1/3)x^3/2 + (5/3)x^½ - x^-½ (using the laws of indices).

So differentiating term by term: ½ x^½ + (5/6)x^-½ + ½x^-3/2.

Q1. Both the derivative and the integral of this function are same

(a) the function is e^x.

(b) the function is e^2x.

(c) the function is 2e^x.

(d) the function is ln x.

Q2. If f(x) = h(g(x)), then f'(x) =

(a) h'(g’(x)). g(x)

(b) h(g’(x)). g'(x)

(c) h'(g(x)). g(x)

(d) h'(g(x)). g'(x)

Q3. The derivative of log_ax is 

(a) 1/x ln ax

(b) 1/x ln ax

(c) 1/x ln ax

(d) 1/x ln ax

Q4. The derivative of a constant function is 

(a) zero

(b) the function itself.

(c) constant

(d) none of these

Q5. the derivative of the function [f(x)]ⁿ is

(a) n f(x)ⁿ (f’(x))

(b) n f’(x)^n-1 (f(x))

(c) n f(x)^n-1 (f’(x))

(d) f(x)^n-1 (f’(x))

Q1.	Q2.	Q3.	Q4.	Q5.
(a)	(d)	(b)	(a)	(c)

Related Resources

• You may wish to refer general theorems on differentiation.

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Methods of Differentiation comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.

More Readings

Logarithmic Differentiation