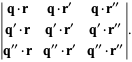Scalar Triple Product

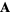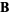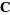The scalar triple product of three vectors , , and is denoted and defined by

			(1)
			(2)
			(3)
			(4)
			(5)

where 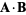denotes a dot product, 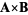denotes a cross product, 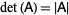denotes a determinant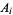, 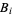and , , and 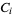are components of the vectors 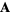, , 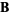and 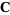, respectively. The scalar triple product is a pseudoscalar (i.e., it reverses sign under inversion). The scalar triple product can also be written in terms of the permutation symbol 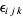as

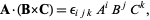(6)

where Einstein summation has been used to sum over repeated indices.

Additional identities involving the scalar triple product are

			(7)
			(8)
			(9)

The volume of a parallelepiped whose sides are given by the vectors 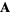, , 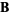and 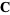is given by the absolute value of the scalar triple product

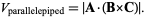(10)

SEE ALSO: Cross Product, Dot Product, Parallelepiped, Vector Multiplication, Vector Triple Product

REFERENCES:

Arfken, G. "Triple Scalar Product, Triple Vector Product." §1.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 26-33, 1985.

Aris, R. "Triple Scalar Product." §2.34 in Vectors, Tensors, and the Basic Equations of Fluid Mechanics. New York: Dover, pp.  18-19, 1989.

Griffiths, D. J. Introduction to Electrodynamics. Englewood Cliffs, NJ: Prentice-Hall, p. 13, 1981.

Jeffreys, H. and Jeffreys, B. S. "The Triple Scalar Product." §2.091 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 74-75, 1988.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 11, 1953.

Referenced on Wolfram|Alpha: Scalar Triple Product

In mathematics, the triple product is a product of three vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product.