Dear Shubham,
The formula for the length of a 2D vector is the Pythagorean Formula. Say that the vector is represented by   (x, y)T.   Put the vector with its tail at the origin. Now make a triangle by drawing the two sides:
side_1   =  (x, 0)T

side_2   = (0, y)T.

The length of side_1 is x, and the length of side_2 is y, so:




length (x, y)T   =    ( x2 + y2 )




In this formula,    means the positive square root. We don''t (of course) want the length to be negative.
Cracking IIT just got more exciting,It s not just all about getting assistance from IITians, alongside Target Achievement and Rewards play an important role. ASKIITIANS has it all for you, wherein you get assistance only from IITians for your preparation and win by answering queries in the discussion forums. Reward points 5 + 15 for all those who upload their pic and download the ASKIITIANS Toolbar, just a simple  to download the toolbar….
So start the brain storming…. become a leader with Elite Expert League ASKIITIANS
Thanks
Aman Bansal
Askiitian Expert
 
						

							
Dear Shubham,
 vector quantity has both magnitude and direction. Acceleration, velocity, force and displacement are all examples of vector quantities. A scalar quantity is has only magnitude (so the direction is not important). Examples include speed, time and distance.
Unit Vectors
A unit vector is a vector which has a magnitude of 1. There are three important unit vectors which are commonly used and these are the vectors in the direction of the x, y and z-axes. The unit vector in the direction of the x-axis is i, the unit vector in the direction of the y-axis is j and the unit vector in the direction of the z-axis is k.
Writing vectors in this form can make working with vectors easier.
The Magnitude of a Vector
The magnitude of a vector can be found using Pythagoras''s theorem.


The magnitude of ai + bj = √(a2 + b2)


We denote the magnitude of the vector a by | a |
Position Vectors
Position vectors are vectors giving the position of a point, relative to a fixed point (the origin).
For example, the points A, B and C are the vertices of a triangle, with position vectors a, b and c respectively:

You can draw in the origin wherever you want. 
Notice that  = - a + b = b - a because you can get from A to B by going from A to O and then going from O to B.
Cracking IIT just got more exciting,It s not just all about getting assistance from IITians, alongside Target Achievement and Rewards play an important role. ASKIITIANS has it all for you, wherein you get assistance only from IITians for your preparation and win by answering queries in the discussion forums. Reward points 5 + 15 for all those who upload their pic and download the ASKIITIANS Toolbar, just a simple  to download the toolbar….
So start the brain storming…. become a leader with Elite Expert League ASKIITIANS
Thanks
Aman Bansal
Askiitian Expert
 
						

							
Vector Formulas
A vector can also be defined as an element of a vector space.  Vectors are sometimes referred to by the number of coordinates they have, so a 2-dimensional vector  is often called a two-vector, an n-dimensional vector is often called an n-vector, and so on.
The important formulas of vectors are given below:
 
1. The position vector of any point p(x,y) is
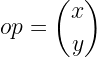 or OP = ( x,y ).
 
2.The magnitude of position vector
 and direction 
 
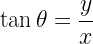
3. The unit vector = 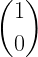 where the magnitude of unit vector is 1
Or,the unit vector = 
 
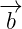4.The two vectors  and  are parallel if  and 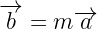 where k and m are the scalars.
 
5.If  then  is the result vector which is the triangle law of vector addition.
 
6. The scalar or dot product of any two vectors .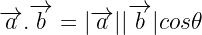
 
7. The angle between two vectors is 
 
8.  and  , then :
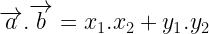 where 
 
9. If the position vector of A is  , position vector of point B is 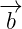 and position vector of mid-point M is m then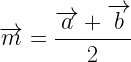 
 
10. If the point P divides Ab internally in the ratio m:n then position vector of P is given by  which is a section formula.
 
11.If P divides AB externally in the ratio m:n then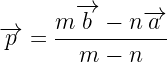 

PRODUCT OF TWO VECTORS
 
1.Scalar Product ( dot product )
 
Let  then dot product of  &  is devoted by  read as  dot  and defined by 
 
Note:
if
 
OR
 
The scalar product of  &  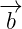is devoted by  ,
 where  being  angle between  & 
 
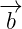
Note:1

Note:2
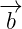 &  are perpendicular if  = 
i.e 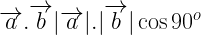 or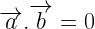 
 
2.Properties of Scalar Product
i. .
ii. .
iii. 
iv. 
v. If then 
 
3.Vector (cross) Product of two vectors.
Let 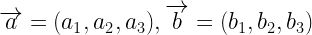 be two vectors then the cross product of 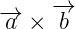is devoted by 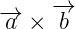and defined by
 
 = 
 
We can define in terms of determinants as follows
 
 = 
 
Note:1                being angle between
 & 
Note:2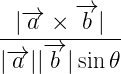               
Note:3               If 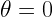 , the  and  &  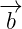are parallel if .
 
4. Properties of cross product
 
i. 
ii. 
iii.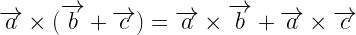 
iv.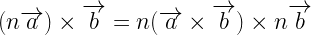 
v. 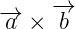 is perpendicular to both  and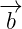 
vi. 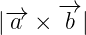 is a Area of paralelogram with sides  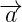and 
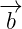vii.  = area of triangle having  ,  ,  as position vectors of vertices of a triangle.