The smallest possible root of the equation tan x = x lies in which interval?? Q3 above
The smallest possible root of the equation tan x = x lies in which interval?? Q3 above
Sandipkumar , 6 Years ago
Grade 11
Trigonometry> The smallest possible root of the equatio...
2 AnswersArun
Last Activity: 6 Years ago
Note that tan x > x in (0, pi/2). It is clear from the graph that the point of intersection lies in the interval (pi/2, 3pi/2) which corresponds to the smallest positive root of tan x - x = 0.
Regards
Arun (askIITians forum expert)
Aditya Gupta
Last Activity: 6 Years ago
consider f(x)= tanx – x
now f ’(x)= sec^2x – 1= tan^2x>=0
now, f(0)=0 so f(x)>0 for all x in (0, π/2)
now, in (π/2. π), f(x) is always negative.
now, f(π)= – π and lim x----> 3π/2- (f(x))= plus infinty
since f(x) is continuous in (π, 3π/2), it has to pass through zero inside this interval
so the smallest positive root lies in (π, 3π/2). option (c)
Provide a better Answer & Earn Cool Goodies
LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.
Full Live Access
Study Material
Live Doubts Solving
Daily Class Assignments
Ask a Doubt
Get your questions answered by the expert for free
Other Related Questions on trigonometry
In ABC, if cot A+cot B+cot C = cosecA cosecB cosecC, then prove that ABC is right angle triangle.
In ABC, if cot A+cot B+cot C = cosecA cosecB cosecC, then prove that ABC is right angle triangle.
trigonometry
1 Answer Available
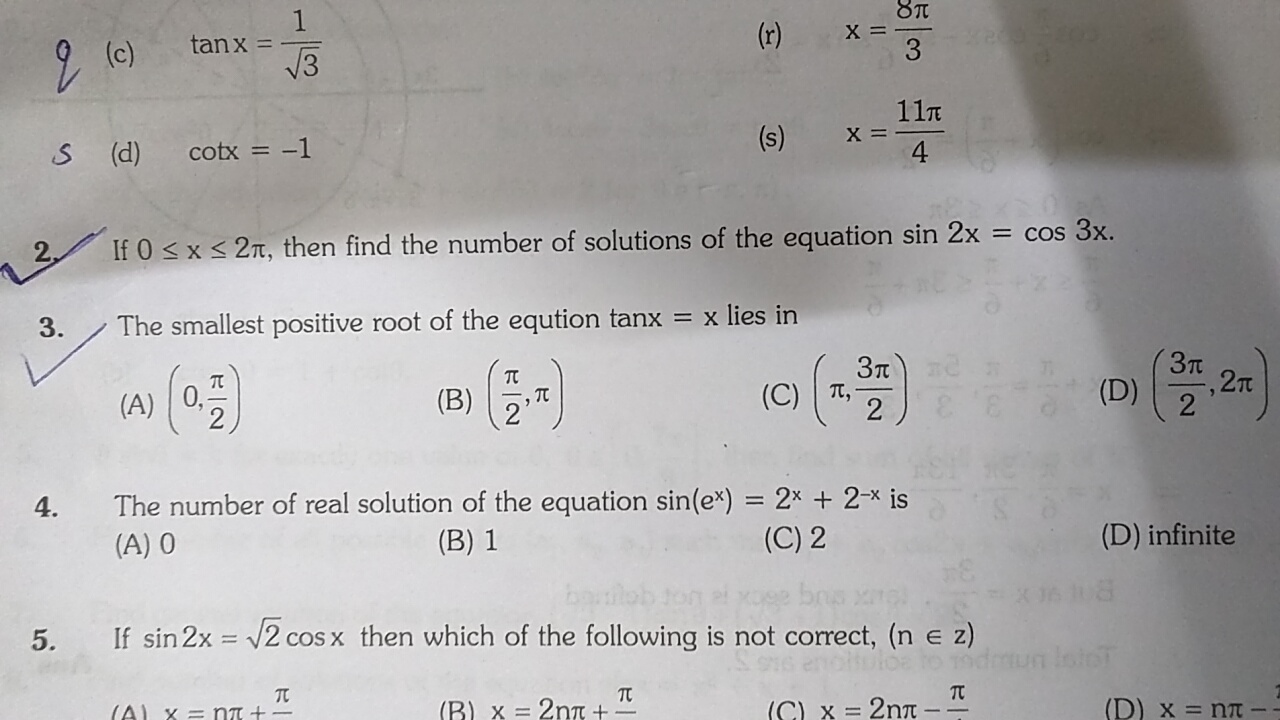
Last Activity: 2 Years ago
- Find the general solution of equation tan3∂=cot2∂
For all angles between -720 and +720
- Find the general solution of equation tan3∂=cot2∂
For all angles between -720 and +720
trigonometry
0 Answer Available
Last Activity: 3 Years ago
To prove : Cosec(45 degree - A)Cosec(45 degree + A) = 2SecA
To prove : Cosec(45 degree - A)Cosec(45 degree + A) = 2SecA
trigonometry
0 Answer Available
Last Activity: 3 Years ago
cos^2 13ºcos^2 47º+cos^2 73º =? …..................
cos^2 13ºcos^2 47º+cos^2 73º =? …..................
trigonometry
0 Answer Available
Last Activity: 3 Years ago
Derive a formula for the area of the triangle, given b, A, B, and C. That is, derive the formula: (b^2sinAsinC)/(2sinB)
Derive a formula for the area of the triangle, given b, A, B, and C. That is, derive the formula: (b^2sinAsinC)/(2sinB)
trigonometry
0 Answer Available
Last Activity: 3 Years ago