Please Solve this ques with proper reasons....?.........................

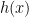Suppose  is a twice differentiable, real-valued function on an interval  and that  for all . Then, for every positive integer m and for all points 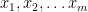 in , we have

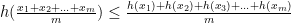
Moreover, equality holds if and only if 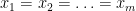. A similar result holds if

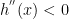 for all  except that the inequality sign is reversed.

now, if we set h(x)=sinx, h’(x)=cosx or h”(x)= – sinx. it is given in question that x1, x2, …..xn lie in the interval (0,π). in ths interval, sinx is positive, implying h”(x)

so, h((x1+x2+...xn)/n)=sin(π/n) >= (sinx1+sinx2+....sinxn)/n

so, the greatest value of the sum turns out to be n*sin(π/n), which occurs when all xi’s are equal to each other.