0

Guest

Courses New

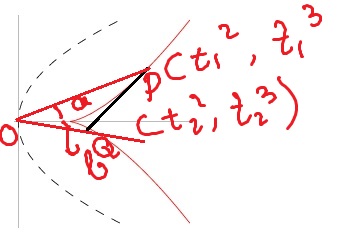
If the tangent at point P of the curve, y^2=x^3 intersects the curve again at point Q and the straight lines OP,OQ make angles a,b withe x axis where O is origin, then tan(a)/tan(b) has a value- (1.) -1 (2). -2 (3). 2 (4). 2^(.5)

If the tangent at point P of the curve, y^2=x^3 intersects the curve again at point Q and the straight lines OP,OQ make angles a,b withe x axis where O is origin, then tan(a)/tan(b) has a value-


(1.) -1    (2). -2    (3). 2       (4).  2^(.5)

Grade:12

1 Answers

Sumit Majumdar IIT Delhi
askIITians Faculty 137 Points
9 years ago
Solution:
68-2070_1.jpg
Let us assume the parametric coordinates at P and Q be:
\left (t_{1}^{2}, t_{1}^{3} \right ), \left (t_{2}^{2}, t_{2}^{3} \right )
Now finding the slope of the tangent at the point P, we get:
\frac{dy}{dx}=\frac{3x^{2}}{2y}=\frac{3}{2t_{1}}
Also the line joining P and Q would have a slope given by:
\frac{t_{2}^{3}-t_{1}^{3}}{t_{2}^{2}-t_{1}^{2}}
equating both the slopes would give:
2t_{2}^{2}=t_{1}\left ( t_{2}+t_{1} \right )
This can futher be simplified as:
2\frac{t_{2}^{2}}{t_{1}^{2}}=\frac{t_{2}}{t_{1}}+1
Also, we have:
tan(a)=t_{1} tan(b)=t_{2}
Using these we get the required result.
Thanks & Regards
Sumit Majumdar,
askIITians Faculty
Ph.D,IIT Delhi

Think You Can Provide A Better Answer ?

Other Related Questions on Trigonometry

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More