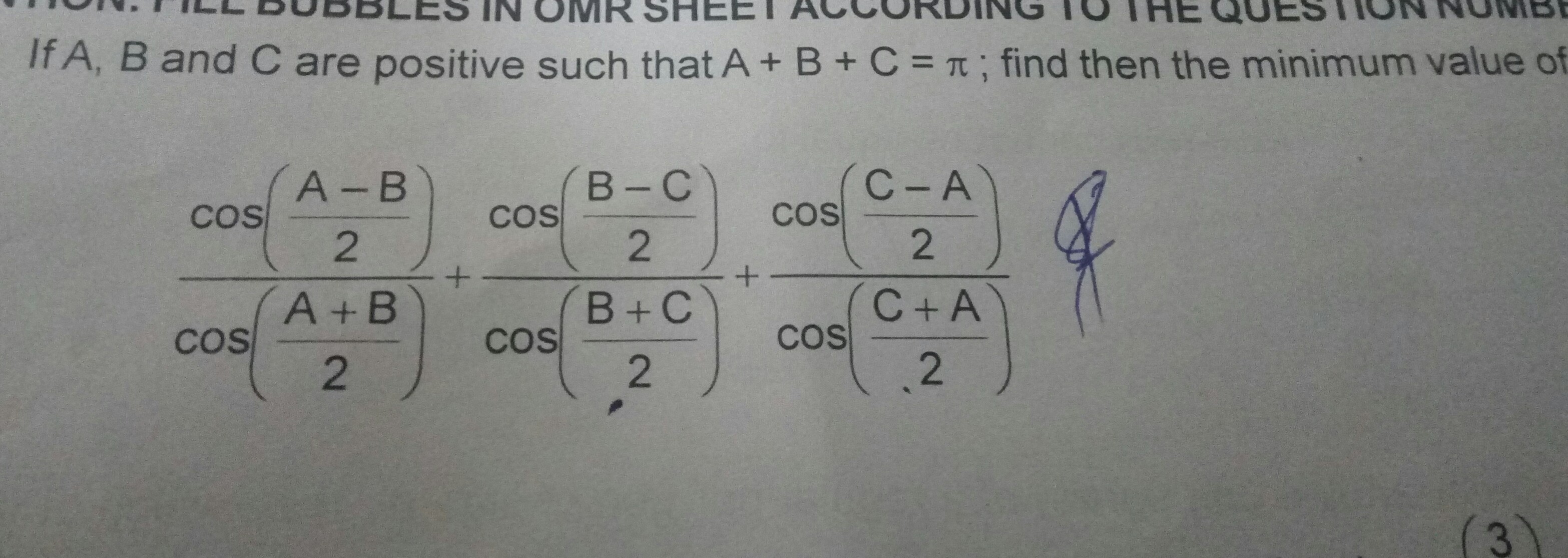
Conditional IdentityTried to solve itBut not getting Needing help
Rshuj , 6 Years ago
Grade 11
Trigonometry> Conditional Identity Tried to solve it Bu...
1 Answers
Aditya Gupta
Last Activity: 6 Years ago
i know its a tough one, but bear with me.
consider cos(A-B)/2/cos(A+B)/2
multiply numerator and denominator by 2sin(A+B)/2
so it becomes (sinA+sinB)/(sin(A+B)).......[coz sin2x=2sinxcosx and sinx+siny=2sin(x+y)/2cos(x-y)/2]
but sin(A+B)=sin(180-C)=sinC
so, the sum can be written as
(sinA/sinC+sinC/sinA)+(sinA/sinB+sinB/sinA)+(sinB/sinC+sinC/sinB)
assuming A, B and C are angles of a triangle, by sin we can write it as:
(a/c+c/a)+(b/a+a/b)+(b/c+c/b)
but x+1/x>=2 whenever x>0
so a/c+c/a>=2
b/a+a/b>=2
and b/c+c/b>=2
ADding, we get
sum>=6, which is attained when A=B=C=60degree
so, the minimum value of the sum is 6.
Provide a better Answer & Earn Cool Goodies
Enter text here...
LIVE ONLINE CLASSES
Prepraring for the competition made easy just by live online class.
Full Live Access
Study Material
Live Doubts Solving
Daily Class Assignments
Ask a Doubt
Get your questions answered by the expert for free
Enter text here...
Other Related Questions on Trigonometry
In ABC, if cot A+cot B+cot C = cosecA cosecB cosecC, then prove that ABC is right angle triangle.
Trigonometry
1 Answer Available
Last Activity: 2 Year ago(s)
\tFind the general solution of equation tan3∂=cot2∂For all angles between -720 and +720
Trigonometry
0 Answer Available
Last Activity: 2 Year ago(s)
To prove : Cosec(45 degree - A)Cosec(45 degree + A) = 2SecA
Trigonometry
0 Answer Available
Last Activity: 2 Year ago(s)
cos^2 13ºcos^2 47º+cos^2 73º =? …..................
Trigonometry
0 Answer Available
Last Activity: 2 Year ago(s)
Derive a formula for the area of the triangle, given b, A, B, and C. That is, derive the formula: (b^2sinAsinC)/(2sinB)
Trigonometry
0 Answer Available
Last Activity: 2 Year ago(s)