0

Guest

Courses New

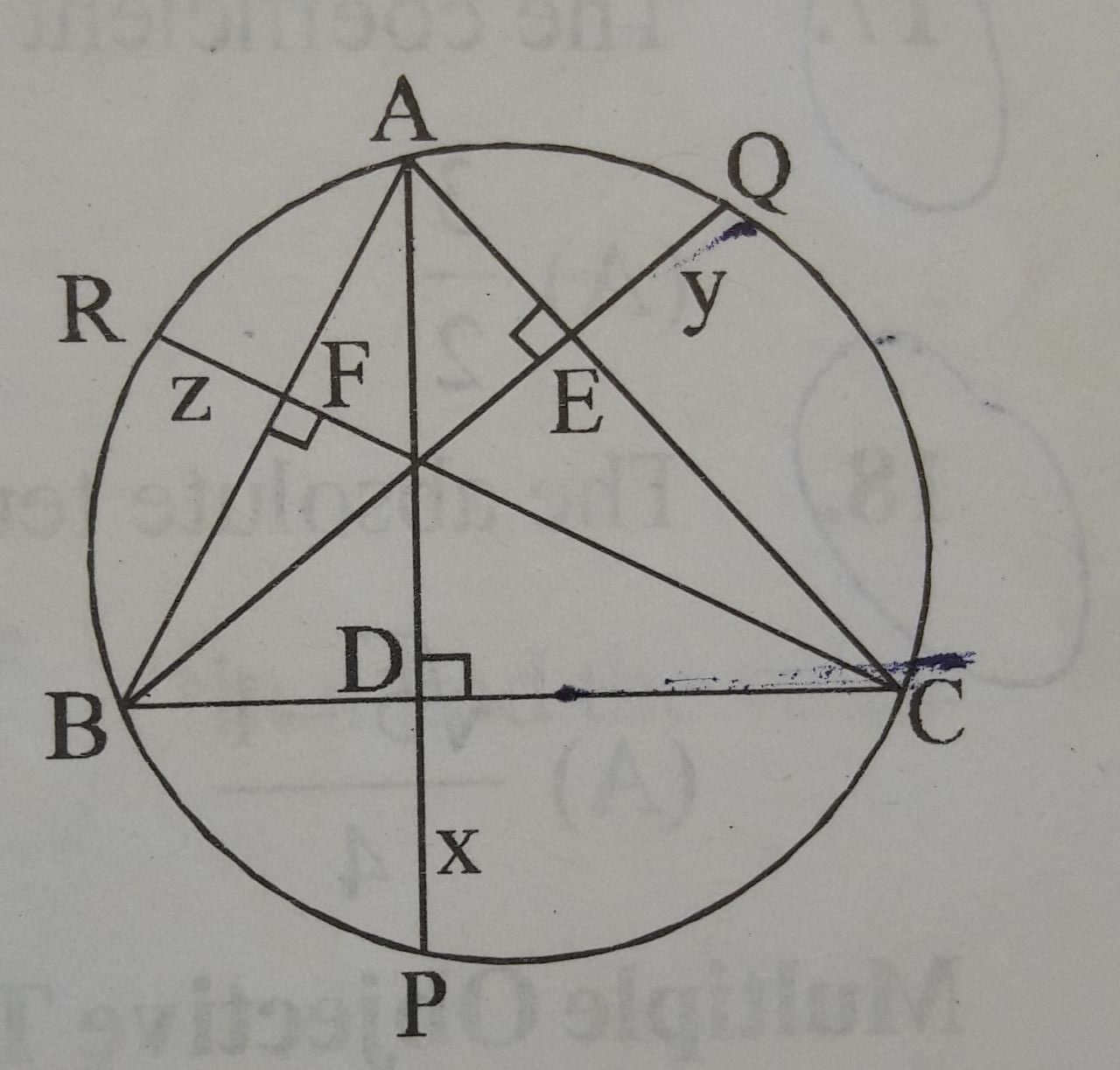
as shown in the figure AD is the altitude on BC and AD produced meets the circumcircle of traingle ABC at P where DP =x . similarly EQ=y and FR = z . if a, b ,c respectively denotes the sides BC, CA, and AB , then a/2x+b/2y+c/2z has the value equal to

as shown in the figure AD is the altitude on BC and AD produced meets the circumcircle of traingle ABC at P where DP =x . similarly EQ=y and FR = z . if a, b ,c respectively denotes the sides BC, CA, and AB , then a/2x+b/2y+c/2z has the value equal to

Question Image
Grade:

1 Answers

Aarushi Ahlawat
41 Points
5 years ago
Use the intersection chord theorem to get relation between a/2x, b/2y and c/2z. NOw write a, b, and c as sum of two parts of the side e.g a=BD+DC and so on. Convert the ratios to trigonometric ratios of specific angle and you should get answer in the form of sum of trigonometric ratios of the angle angles. Further simplication is possible with the fact that A+B+C=pi.
 
for Two intersecting chords BC and AP
 
AD X x=BD X DC
 
\frac{a}{2x}=\frac{(BD+ DC)AD}{2BDXDC}
 
=\frac{1}{2}\left ( \frac{AD}{DC}+\frac{AD}{BD} \right )
=\frac{1}{2}\left ( tan(C)+tan(B) \right )
 
similarly 
 
\frac{b}{2y}=\frac{1}{2}\left ( tan(A)+tan(C) \right )
\frac{c}{2z}=\frac{1}{2}\left ( tan(A)+tan(B) \right )
 
Hence
 
\frac{a}{2x}+\frac{b}{2y}+\frac{c}{2z}=tan(A)+tan(B)+tan(C)

Think You Can Provide A Better Answer ?

Other Related Questions on Trigonometry

View all Questions »

ASK QUESTION

Get your questions answered by the expert for free

Answer and earn gift vouchers

Win Gift vouchers upto Rs 500/-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Complete Self Study Package designed by Industry Leading Experts

Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child

Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Click Here Know More