Adsorption is often used as a polishing step to provide advanced treatment for hardly degradable substances present in secondary effluents. An activated was obtained and batch adsorption experiments were carried out to establish adsorption isotherm for the carbon. The data given in Table 1 represent equilibrium chlorbbenzene (CB) concentrątionş obtained in batch adsorption experiments where 1 g of activated carbon was added into each of seven beakers containing 1 liter of wastewater with varying initial chlorobenzene concentrątion.

Given:

Contaminant = chlorobenzene [C6H5CL] (CB)

BC Saturation concentration = 500 mg/L

1. Derive the adsorption constants using the

a) Freundlich model

b) Langmuir model

c) BET model

Use a spreadsheet to analyze the datá and establish which model describes best adsorption on the given carbon and why? Tabulate your answers of experimental constants for each model along with the appropriate regression parameter

1. Based on the analysis above which carbon would you recommend for effective removal of chlorobenzene and why?

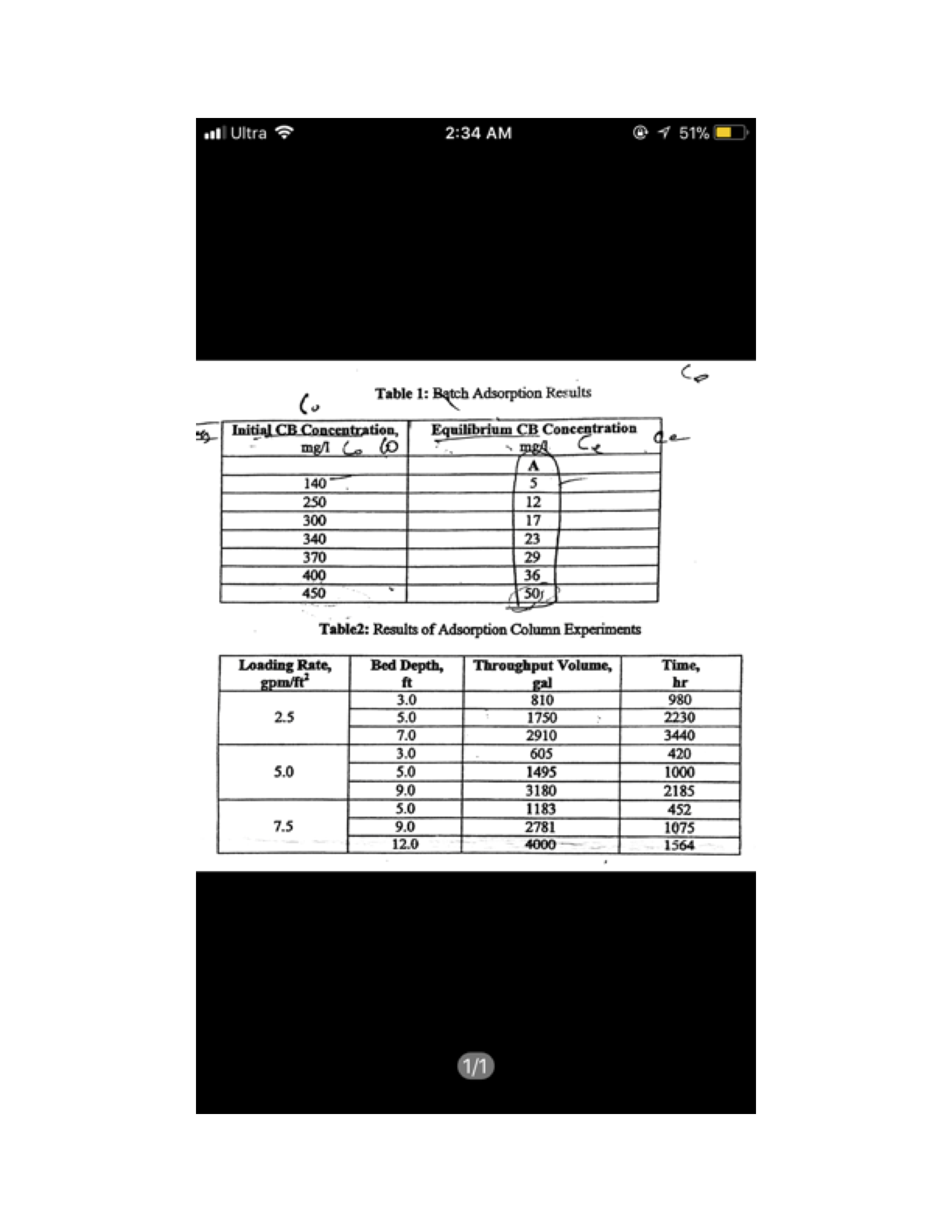
Adsorption is a critical process in wastewater treatment, especially for removing contaminants like chlorobenzene (CB), which can be challenging to degrade biologically. In your scenario, you've conducted batch adsorption experiments using activated carbon to establish adsorption isotherms. Let's break down how to derive the adsorption constants using the Freundlich, Langmuir, and BET models, and analyze which model best describes the adsorption behavior of chlorobenzene on the activated carbon.

Understanding the Adsorption Models

Each adsorption model provides a different perspective on how contaminants interact with adsorbents. Here’s a brief overview of the three models:

• Freundlich Model: This empirical model is suitable for heterogeneous surfaces and is expressed as: q = Kf * C^1/n, where q is the amount adsorbed, C is the equilibrium concentration, Kf is the Freundlich constant, and n is a measure of adsorption intensity.
• Langmuir Model: This model assumes monolayer adsorption on a surface with a finite number of identical sites. The equation is: q = (Qm * b * C) / (1 + b * C), where Qm is the maximum adsorption capacity and b is the Langmuir constant.
• BET Model: This model extends the Langmuir theory to multilayer adsorption and is expressed as: 1 / (V[(P0/P) - 1]) = (1 / (Vm * C)) * (P/P0) + (1 / (Vm * C)), where V is the volume of gas adsorbed, P0 is the saturation pressure, P is the equilibrium pressure, and Vm is the volume of gas adsorbed at monolayer coverage.

Deriving Adsorption Constants

To derive the constants for each model, you will need to analyze the data from your batch experiments. Here’s how you can do it:

1. Data Preparation

Input your experimental data into a spreadsheet. You should have columns for initial chlorobenzene concentration, equilibrium concentration, and the amount of chlorobenzene adsorbed.

2. Freundlich Model Calculation

Using the Freundlich equation, you can plot log(q) against log(C). The slope of the line will give you 1/n, and the intercept will provide log(Kf). From this, you can calculate Kf and n.

3. Langmuir Model Calculation

For the Langmuir model, rearrange the equation to linear form: 1/q = (1/(Qm * b)) * (1/C) + (1/Qm). Plot 1/q against 1/C. The slope will give you 1/(Qm * b) and the intercept will give you 1/Qm.

4. BET Model Calculation

For the BET model, you will need to plot 1 / (V[(P0/P) - 1]) against P/P0. The slope and intercept from this plot will help you derive Vm and C.

Model Comparison and Analysis

Once you have calculated the constants for each model, you can assess which model fits your data best by looking at the regression parameters, such as R-squared values. The model with the highest R-squared value indicates the best fit for your adsorption data.

Recommendations for Effective Removal

Based on your analysis, if the Langmuir model shows the best fit, it suggests that the adsorption of chlorobenzene on the activated carbon is likely monolayer and occurs at specific sites. If the Freundlich model fits better, it indicates a heterogeneous surface with varying affinities for chlorobenzene. The BET model would imply multilayer adsorption, which may be beneficial for certain applications.

Ultimately, the choice of activated carbon for effective removal of chlorobenzene should consider the model that best describes the adsorption behavior. If the Langmuir model is most applicable, a carbon with a high Qm value would be recommended for its capacity to adsorb chlorobenzene efficiently. If the Freundlich model is more suitable, then a carbon with a high Kf value would be preferable for its effectiveness at lower concentrations.

In summary, your analysis will guide you in selecting the most effective activated carbon for chlorobenzene removal based on the adsorption characteristics revealed by the models.