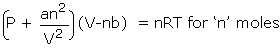where a and b are Vanderwaals constants.  The constant 'a' measures the forces of attraction between the molecules of the gas and 'b' relates to the incompressible volume of the molecules, measuring the size of the gas molecules.

for n = 1

PV = P(b) + { a/V - ab/V² +RT}

its of form y=mx+c where c is Y - intercept

Y - intercept : { a/V - ab/V² +RT}

--

Please feel free to post as many doubts on our disucssion forum as you can. If you find any question difficult
to understand - post it here and we will get you the answer and detailed solution very quickly.We are all
IITians and here to help you in your IIT JEE preparation. All the best.

Regards,
Ramesh
IIT Kgp - 05 batch

Hi Rajat,

The gas law in case of ideal state is : PV=nRT , this is not beyed by real gases

in ideal gases, we assume volume of gas molecule as negligible and we say tootal volume as V

and similarly, the pressure of these gas molecules is also not considered, so its taken as P;

but for ideal gas,we shldn't neglect this extar pressure and volume of them

so ,considering these, we have equation of gas i.e. Real gas as stated by vanderwaals is

(P + (an²/V²))(V - nb) =nRT

since its given as molar volume, we will take n=1 mole

for n=1

(P + a/V² )( V - b ) = RT

PV - Pb + a/V - ab/V² = RT

PV =  Pb - a/V + ab/V² + RT

(PV) =  (P)b - a/V + ab/V² + RT

It is of form: Y = mX + C

where y-intercept C is :   ab/V² - a/V + RT

please understand that there is no real physics or chemistry involved here... take the vanderwaals equation in (p=..)(v-nb)= nrt form...

assume pv = y and p= x

now all u have to do is manipulate the equation to come to the form of y=mx+c --> which is a standard equation for straight line plot.

that is all - rearrange the vanderwaals equation in y=mx+c form and what you get in place of c is the y intercept.

you will find that the answer you will obtain is a/V - ab/V² +RT

now most importantly, the confusion arises as to why we do this silly mathematical trick and why it is important. I assume once you understand that, this simple trick of converting this second degree to straight line will come to you automatically.

this is important because, in experimental setup, we  have to take a few samples and then plot the curve to obtain the relationship.

this will automatically lead to an error(very clearly, you cannot plot a graph unless you have all the points - unless the graph is continuous)

for straight line you just need two points to determine it completely- to obtain its complete equation. wheras for a second degree equation you need minimum three points. and considering experimental error etc, it is as good to have as many points as possible . once you have so many points, you need to know the mathematical methods to decrease error. these techniques are best known for straight line plots - things lik e regression analysis etc can be used to accurately decide the equations.

hence, most empirical relations(of which vanderwaals eqn is one) are preferred in straight line form. that is all there is..

you will find that the ans in the book is RT this is so because as 'a' and 'b' are very small therefore we can neglect the terms ab/v^2  and a/v