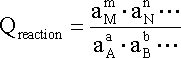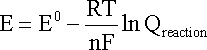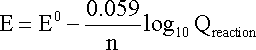ONE half cell in a voltaic cell is constructed from a silver wire dipped in a silver nitrate solution of unknown concentration. its other half cell consists of a zinc electrode dipped in 1.0 M solutionof zinc nitrate. a voltage of 1.48 is measured for this cell. calculate concentration of silver nitrate. {standard electrode potentials are given: Zn2+\\\\Zn= -0.76 V . Ag+\\\\Ag = 0.80 V.}

Dear student,

where, for a generalized equation of the form:

The capital letters A, B, M and N in equation represent respectively the reactants and products of a given reaction while the small letters represent the coefficients required to balance the reaction.

At equilibrium, DG = 0 and Q_reaction corresponds to the equilibrium constant (K_eq) described earlier.

In the case of an electrochemical reaction, substitution of the relationships DG = -nFE and D

Combining constants at 25^oC (298.15 K) gives the simpler form of the Nernst equation for an electrode reaction at this standard temperature:

In this equation, the electrode potential (E) would be the actual potential difference across a cell containing this electrode as a half-cell and a standard hydrogen electrode as the other half-cell. Alternatively, the relationship in equation can be used to combine two Nernst equations corresponding to two half-cell reactions into the Nernst equation for a cell reaction: